Lösung von Aufg. 11.05 SoSe 13
Aus Geometrie-Wiki
Version vom 18. Juli 2013, 23:02 Uhr von *m.g.* (Diskussion | Beiträge)
Aufgabe 10.05Beweisen Sie: Jedes Dreieck hat genau einen Umkreis.
LösungExistenzEs sei EindeutigkeitIndirekt mit Widerspruch.--*m.g.* 00:02, 19. Jul. 2013 (CEST) Zurück zu: Serie 11 SoSe 2013 |
 ein Dreieck mit den schulüblichen Bezeichnungen. Zunächst schneiden sich die Mittelsenkrechten
ein Dreieck mit den schulüblichen Bezeichnungen. Zunächst schneiden sich die Mittelsenkrechten 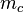 und
und 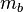 im Punkt
im Punkt  . (Wären sie parallel, müssten auch
. (Wären sie parallel, müssten auch  und
und 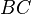 parallel sein und
parallel sein und 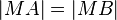 und
und 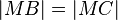 . Nach der Tarnsitivität der Gleicheitsrelation gilt nun:
. Nach der Tarnsitivität der Gleicheitsrelation gilt nun: 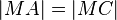 . Nach dem Mittelsenkrechtenkriterium geht jetzt
. Nach dem Mittelsenkrechtenkriterium geht jetzt  ist nun der gesuchte Umkreis.
ist nun der gesuchte Umkreis.
