14)

a) Geben Sie die Menge $M$ aller konvexer Drachenvierecke an.
b) Bilden Sie das kartesische Produkt der Menge $M \times M$.
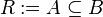c) Wir definineren eine Relation $R$ mit $R:=A\subseteq B$. Bestimmen Sie die Relation $R$ auf $M \times M$.
d) Untersuchen Sie die Relation $R$ auf ihre Eigenschaften (reflexiv, symmetrisch, transitiv).

• Sollen wir hier in dem Fall den schiefen Drachen auch nehmen? Ich würde sagen JA, bin mir allerdings nicht sicher. --Der Kuckuck 19:57, 24. Nov. 2013 (CET)
• Es ist nur die Menge der symmetrischen Drachen gemeint. Die Aufgabe ist aber nicht falsch, wenn du von der Menge der schiefen Drachen ausgehst.--Tutorin Anne 10:11, 25. Nov. 2013 (CET)

zu a) M={Drache schief, Drache, Raute, Quadrat}
zu b) M x M={(D_s, D_s), (D_s,D),(D_s,R_A), (D_s,Q), (D,D_s),(D,D), (D,R_A), (D,Q), (R_A, D_s), (R_A,D), (R_A,R_A), (R_A,Q), (Q,D_s), (Q,D), (Q, R_A), (Q,Q)}

• Richtig, 16 Paare! Es war ein kleiner Tippfehler drin, so dass (Q,Q) zwei Mal vorkam - den habe ich korrigiert.--Tutorin Anne 10:55, 28. Nov. 2013 (CET)

zu c) R={(D,D_s), (R_A,D_s), (R_A,D), (Q,R_A), (Q,D), (Q,D_s)}

• Das sind noch nicht alle Paare, die zu dieser Relation gehören. Es sind aber keine Falschen drin.--Tutorin Anne 10:55, 28. Nov. 2013 (CET)

zu d) R ist nicht reflexiv und nicht symmetrisch--Smartie 15:39, 26. Nov. 2013 (CET)

• Du schreibst reflexiv. Auf deine in c) beschrieben Relation trifft das allerdings nicht zu. Was ist mit transitiv?--Tutorin Anne 10:55, 28. Nov. 2013 (CET)