Übung 03.02.
Inhaltsverzeichnis[Verbergen] |
Bemerkung
Wir werden nicht alle Aufgaben ausführlich besprechen können. Bereitet euch inhaltlich auf die Übung vor, sodass wir die Aufgaben durchgehen können und ausgewählte davon besprechen, die anderen ggf. Lösungen vergleichen. Das bedeutet: Versucht euch die Lösungswege aller Aufgaben klarzuwerden, sodass wir darüber reden können. Wir werden nicht alle einzelnen Rechenschritte durchgehen.
Aufgabe 1
a) Prüfen Sie, ob die Vektoren 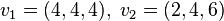 und
und 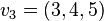 ein Erzeugendensystem von
ein Erzeugendensystem von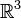 bilden.
bilden.
b) Untersuchen Sie, für welche 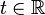 die Vektoren
die Vektoren 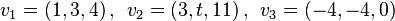 linear abhängig in
linear abhängig in 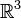 sind.
sind.
Aufgabe 2
Zeigen Sie, dass die Vektoren 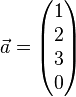 ,
, 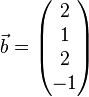 ,
, 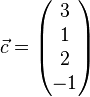 und
und 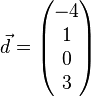 linear abhängig sind und überprüfen Sie, welche(r) der Vektoren sich als Linearkombination der jeweils anderen drei Vekotren darstellen lässt/lassen.
linear abhängig sind und überprüfen Sie, welche(r) der Vektoren sich als Linearkombination der jeweils anderen drei Vekotren darstellen lässt/lassen.
Aufgabe 3
Geben Sie zu folgenden Polynomen die Linearkombination (bzw. die Koordinaten) bzgl folgendem Erzeugendensystems 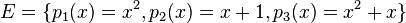 an.
an.
a) 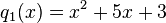
b)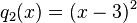
c)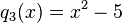
Aufgabe 4
Bestimmen Sie eine Basis des von der Menge erzeugenten Vektorraum U=<X>.
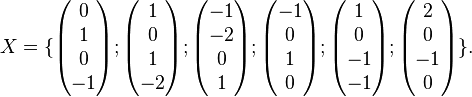
Gilt 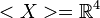 ?
?
Aufgabe 5
Geben Sie für folgende Vektorräume eine Basis an:
a) 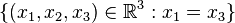
b)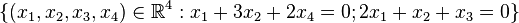
Aufgabe 6
Konstruieren Sie eine Basis für den von
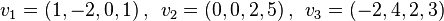
erzeugten Vektorraum und ergänzen Sie diese Basis zu einer Basis von 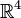 .
.

