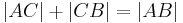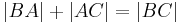14)
Aus Geometrie-Wiki
Version vom 5. Februar 2014, 10:16 Uhr von Tutorin Anne (Diskussion | Beiträge)
Beweisen Sie: Es sei  mit
mit  sind paarweise verschieden.
sind paarweise verschieden.
Dann gilt genau eine der folgenden Zwischenrelationen:  oder
oder 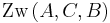 oder
oder 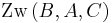 .
.
Aus der Dreiecksungleichung
- "Für drei beliebige Punkte
 und
und  gilt:
gilt: 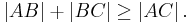
- "Für drei beliebige Punkte
- Falls
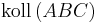 , dann ist eine der folgenden Gleichungen erfüllt:
, dann ist eine der folgenden Gleichungen erfüllt:
- Falls
- Ist umgekehrt eine dieser drei Gleichungen erfüllt, so sind
 ,
,  und
und  kollinear."
kollinear."
folgt unmittelbar unter Verwendung von der Definition I.2: (Zwischenrelation)
- "Ein Punkt
 liegt zwischen zwei Punkten
liegt zwischen zwei Punkten  und
und  , wenn
, wenn  gilt und der Punkt
gilt und der Punkt  sowohl von
sowohl von  als auch von
als auch von  verschieden ist.
verschieden ist.
- "Ein Punkt
- Schreibweise:
 "
"
- Schreibweise:
die Behauptung.
--EarlHickey (Diskussion) 13:19, 4. Feb. 2014 (CET)
So einfach ist der Beweis leider nicht. Du hast zwar richtig begründet, dass eine Zwischenrelation gilt, jedoch nicht dass genau eine - also nicht zwei auf einmal gelten. < \span> --Tutorin Anne (Diskussion) 10:16, 5. Feb. 2014 (CET)