14)
Gegeben seien drei paarweise verschiedene und kollineare Punkte A, B und C in einer Ebene E. Ferner sei eine Gerade g Teilmenge der Ebene E, wobei keiner der Punkte A, B und C auf g liegen möge. Beweisen Sie folgenden Zusammenhang:
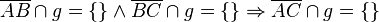
(Hinweis: Nehmen Sie einen weiteren Punkt D an, mit 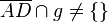 und nutzen Sie den Satz von Pasch)
und nutzen Sie den Satz von Pasch)
1.) Wir betrachten das Dreieck 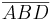
2.) 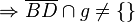
- | Vor.; "Pasch"; 1.)
- | Vor.; "Pasch"; 1.)
3.) Wir betrachten das Dreieck 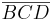
4.) 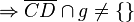
- | Vor.; "Pasch"; 2.); 3.)
- | Vor.; "Pasch"; 2.); 3.)
5.) Wir betrachten das Dreieck 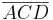
6.) 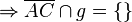
- | Vor.; 4.); 5.); "Pasch"
- | Vor.; 4.); 5.); "Pasch"
--EarlHickey (Diskussion) 14:01, 4. Feb. 2014 (CET)
Der Beweis ist korrekt, sofern du den Hinweis als Schritt 1a) davorsetzt. Du konstruierst als einen Punkt D, für den gilt 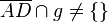 . In deinem Schritt 2) musst du dich dann auf diesen Schritt 1a) berufen, wenn du den Satz von Pasch verwenden möchtest.
. In deinem Schritt 2) musst du dich dann auf diesen Schritt 1a) berufen, wenn du den Satz von Pasch verwenden möchtest.
Danke, EarlHickey!--Tutorin Anne (Diskussion) 10:20, 5. Feb. 2014 (CET)

