14)
Aus Geometrie-Wiki
Version vom 9. Februar 2014, 19:20 Uhr von EarlHickey (Diskussion | Beiträge)
Wie hoch muss ein Spiegel sein, damit Sie sich ganz darin sehen können und auf welcher Höhe muss die Oberkante des Spiegels angebracht werden? Anmerkung: Sie dürfen hier die Strahlensätze, wie sie aus der Schule bekannt sind, verwenden. Tipp: Hier finden Sie eine hilfreiche GeoGebra-Applikation.
- Gegeben sind die Bezeichnungen aus der verlinkten Geogebra-Applikation.
- Gegeben sind die Bezeichnungen aus der verlinkten Geogebra-Applikation.
- Aus den Strahlensätzen lässt sich herleiten:
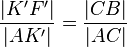 . (1)
. (1)
- Aus den Strahlensätzen lässt sich herleiten:
- Umformen ergibt:
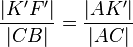 (2)
(2)
- Umformen ergibt:
- Aus den Eigenschaften der Geradenspiegelung ergibt sich:
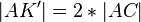 (3)
(3)
- Aus den Eigenschaften der Geradenspiegelung ergibt sich:
- Aus (2) und (3) folgt unmittelbar:
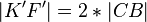
- Aus (2) und (3) folgt unmittelbar:
- Der Spiegel ist also (mindestens) halb so hoch wie die Person.
- Analog kann man herleiten, dass
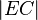 halb so groß ist wie
halb so groß ist wie 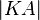 und
und
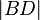 halb so groß ist wie
halb so groß ist wie 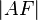 .
.
- Der Spiegel ist also (mindestens) halb so hoch wie die Person.
--EarlHickey (Diskussion) 19:20, 9. Feb. 2014 (CET)

