14)
Aus Geometrie-Wiki
Version vom 14. Februar 2014, 09:33 Uhr von Tutorin Anne (Diskussion | Beiträge)
Zeigen Sie, dass die Verkettung einer Drehung 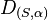 mit einer Verschiebung wieder eine Drehung
mit einer Verschiebung wieder eine Drehung 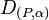 ergibt. Wo liegt das neue Drehzentrum P?
ergibt. Wo liegt das neue Drehzentrum P?
- (1)
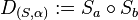
- (2) Verschiebung
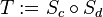
- (3) Es sei
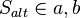
- (4) Drehe
 und
und  so um
so um 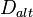 , dass
, dass 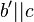 gilt. Es entsteht
gilt. Es entsteht 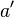 und
und 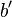
- (5) Verschiebe
 und
und  so, dass
so, dass  auf
auf 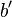 fällt. Es entsteht
fällt. Es entsteht 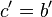 und
und 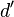 .
.
- (6)
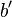 und
und 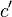 heben sich auf (involutorisch!).
heben sich auf (involutorisch!).
- (7) Der Punkt
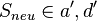 ist der neue Drehpunkt der resultierenden Drehung.
ist der neue Drehpunkt der resultierenden Drehung.
- --EarlHickey (Diskussion) 11:25, 10. Feb. 2014 (CET)
- (1)
Gute Beschreibung deiner Konstruktion. Mit einer Skizze und Bezeichnungen kann es sich jeder veranschaulichen. Es fehlt noch die Begründung, dass es sich bei der neuen vereinfachten Verkettung wieder um eine Drehung mit selbem Winkelmaß handelt. --Tutorin Anne (Diskussion) 13:52, 10. Feb. 2014 (CET)
- Der neue Drehwinkel ist gleich groß, denn
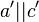 , dadurch bilden die Winkel
, dadurch bilden die Winkel 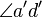 und
und 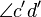 Stufenwinkel. Sie sind also kongruent.--EarlHickey (Diskussion) 22:55, 13. Feb. 2014 (CET)
Stufenwinkel. Sie sind also kongruent.--EarlHickey (Diskussion) 22:55, 13. Feb. 2014 (CET)
- Der neue Drehwinkel ist gleich groß, denn
So ist es. Das besagt der Stufenwinkelsatz.--Tutorin Anne (Diskussion) 09:33, 14. Feb. 2014 (CET)

