Lösung von Zusatzaufgabe 2.5P (SoSe 14)
Welche Definition für Kreis ist richtig? Warum (nicht)?
- Sei
 ein Punkt und
ein Punkt und  eine Menge, deren Elemente Punkte sind. Wenn gilt:
eine Menge, deren Elemente Punkte sind. Wenn gilt:  ist konstant, so ist
ist konstant, so ist  ein Kreis mit Mittelpunkt
ein Kreis mit Mittelpunkt  .
.
- Sei
 ein Punkt und
ein Punkt und  eine Punktmenge. Wenn gilt:
eine Punktmenge. Wenn gilt: 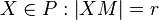 , dann ist
, dann ist  ein Kreis.
ein Kreis.
- Sei
 ein Punkt in der Ebene
ein Punkt in der Ebene  und
und  eine Punktmenge. Wenn
eine Punktmenge. Wenn  alle Punkte
alle Punkte 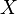 enthält für die gilt∶
enthält für die gilt∶  und
und 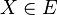 , dann ist
, dann ist  ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  .
.
- Sei
 ein Punkt in der Ebene
ein Punkt in der Ebene  und
und  eine Punktmenge. Wenn
eine Punktmenge. Wenn  genau alle Punkte
genau alle Punkte 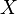 enthält für die gilt∶
enthält für die gilt∶  und
und 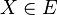 , dann ist
, dann ist  ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  .
.
- Sei
 ein Punkt in der Ebene
ein Punkt in der Ebene  und
und  eine Menge, deren Elemente Punkte sind. Wenn für alle
eine Menge, deren Elemente Punkte sind. Wenn für alle 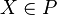 gilt∶
gilt∶  , dann ist
, dann ist  ein Kreis.
ein Kreis.
- Sei
 ein Punkt und
ein Punkt und  eine Menge, deren Elemente Punkte sind. Alle Elemente von
eine Menge, deren Elemente Punkte sind. Alle Elemente von  liegen in ein und derselben Ebene wie
liegen in ein und derselben Ebene wie  . Wenn gilt:
. Wenn gilt:  ist konstant, so ist
ist konstant, so ist  ein Kreis mit Mittelpunkt
ein Kreis mit Mittelpunkt  .
.
Lösung:
- Sei
 ein Punkt und
ein Punkt und  eine Menge, deren Elemente Punkte sind. Wenn gilt:
eine Menge, deren Elemente Punkte sind. Wenn gilt:  ist konstant, so ist
ist konstant, so ist  ein Kreis mit Mittelpunkt
ein Kreis mit Mittelpunkt  .
.
- Als erstes dachte ich, dass es eine richtige Definition sein könnte,da mich der konstante Abstand zwischen dem Mittelpunkt und der Menge aller Punkte P verlockt hat. Aber beim genauen hinlesen, merkte ich, dass P Mittelpunkt sein soll und nicht M. liege ich da falsch?--Picksel (Diskussion) 17:53, 11. Mai 2014 (CEST)
- Sei
 ein Punkt und
ein Punkt und  eine Punktmenge. Wenn gilt:
eine Punktmenge. Wenn gilt: 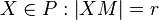 , dann ist
, dann ist  ein Kreis.
ein Kreis.
- Je mehr ich mir die Definitionen anschaue, desto verwirrter werde ich. Jetzt bin mir wegen 1. nicht mehr sicher :) Aber diese Definition könnte richtig sein. --Picksel (Diskussion) 17:53, 11. Mai 2014 (CEST)
- Sei
 ein Punkt in der Ebene
ein Punkt in der Ebene  und
und  eine Punktmenge. Wenn
eine Punktmenge. Wenn  alle Punkte
alle Punkte 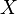 enthält für die gilt∶
enthält für die gilt∶  und
und 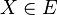 , dann ist
, dann ist  ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  .
.
-Was ist hier dieses R+? --Picksel (Diskussion) 17:53, 11. Mai 2014 (CEST)
- Sei
 ein Punkt in der Ebene
ein Punkt in der Ebene  und
und  eine Punktmenge. Wenn
eine Punktmenge. Wenn  genau alle Punkte
genau alle Punkte 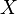 enthält für die gilt∶
enthält für die gilt∶  und
und 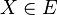 , dann ist
, dann ist  ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  .
.
- Hier auch --Picksel (Diskussion) 17:53, 11. Mai 2014 (CEST)
- Sei
 ein Punkt in der Ebene
ein Punkt in der Ebene  und
und  eine Menge, deren Elemente Punkte sind. Wenn für alle
eine Menge, deren Elemente Punkte sind. Wenn für alle 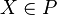 gilt∶
gilt∶  , dann ist
, dann ist  ein Kreis.
ein Kreis.
- Sei
 ein Punkt und
ein Punkt und  eine Menge, deren Elemente Punkte sind. Alle Elemente von
eine Menge, deren Elemente Punkte sind. Alle Elemente von  liegen in ein und derselben Ebene wie
liegen in ein und derselben Ebene wie  . Wenn gilt:
. Wenn gilt:  ist konstant, so ist
ist konstant, so ist  ein Kreis mit Mittelpunkt
ein Kreis mit Mittelpunkt  .
.
-Ich vermute, dass wir diese Aufgabe noch nicht lösen können, da wir über Ebenen noch nicht gesprochen haben.--Picksel (Diskussion) 17:53, 11. Mai 2014 (CEST)

