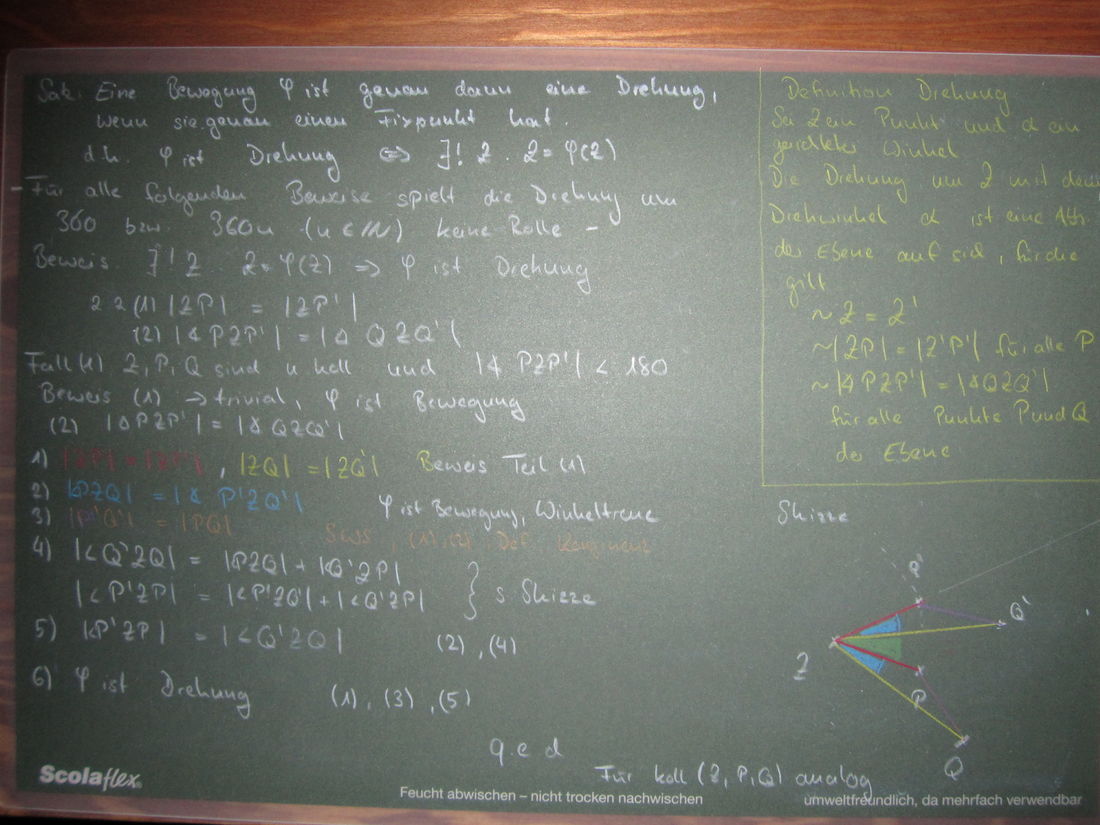12)
Aus Geometrie-Wiki
Version vom 26. Juli 2014, 16:52 Uhr von Wexstabenverbuxler (Diskussion | Beiträge)
Zum Einstieg ein kurzes Quiz
--Flo60 20:52, 19. Nov. 2011 (CET)
Definition Drehung
Voraussetzung ebene Geometrie.
Seien Z ein Punkt der Ebene  und
und  ein gerichteter Winkel.
ein gerichteter Winkel.
Die Drehung mit dem Drehwinkel  um das Drehzentrum Z ist eine Abbildung der Ebene auf sich, für die gilt:
um das Drehzentrum Z ist eine Abbildung der Ebene auf sich, für die gilt:
- Z = Z'
-
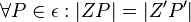
-
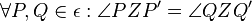
--Flo60 20:52, 19. Nov. 2011 (CET)
Ein' hab ich noch!
Im folgenden wollen wir folgendes Kriterium beweisen, das uns zeigt, dass der Drehung ein Fixpunkt genügt. Dafür müssen wir natürlich die Identität (d. h. jegliche Drehungen um 360°n mit n  |N) ausschließen. Der Satz lautet wie folgt:
|N) ausschließen. Der Satz lautet wie folgt:
Drehungskriterium
Eine Bewegung  ist genau dann eine Drehung, wenn sie genau einen Fixpunkt hat.
ist genau dann eine Drehung, wenn sie genau einen Fixpunkt hat.
 ist Bewegung
ist Bewegung 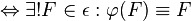
Beweis:
--Flo60 20:52, 19. Nov. 2011 (CET)