15)

a) Geben Sie die Menge $M$ aller konvexer Drachenvierecke an.
b) Bilden Sie das kartesische Produkt der Menge $M \times M$.
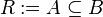c) Wir definineren eine Relation $R$ mit $R:=A\subseteq B$. Bestimmen Sie die Relation $R$ auf $M \times M$.
d) Untersuchen Sie die Relation $R$ auf ihre Eigenschaften (reflexiv, symmetrisch, transitiv).
zu a) M = {s.D., D, P, Ra, Re, Q}

zu b) M x M = {(s.D.,s.D.), (s.D.,D), (s.D.,P), (s.D.,Ra), (s.D.,Re), (s.D.,Q), (D,s.D.), (D,D), (D,P), (D,Ra), (D,Re), (D,Q), (P,s.D.), (P,D), (P,P), (P,Ra), (P,Re), (P,Q), (Ra,s.D.), (Ra,D), (Ra,P), (Ra,Ra), (Ra,Re), (Ra,Q), (Re,s.D.), (Re,D), (Re,P), (Re,Ra), (Re,Re), (Re,Q), (Q,s.D.), (Q,D), (Q,P), (Q,Ra), (Q,Re), (Q,Q)}

zu c) Die Relation R angewendet auf M x M, habe ich in Aufgabe b) dick markiert.

zu d) Die Relation ist reflexiv und transitiv, aber nicht symmetrisch (z.B.: Re ist Teilmenge von P, aber P nicht Teilmenge von Re).