Didaktische Konzepte für die Einführung von Brüchen, 12.05.2015
Inhaltsverzeichnis |
Übung
Definieren Sie den Begriff "Erweitern eines Bruches"
Multipliziert man den Zähler und den Nenner eines Bruches mit derselben natürlichen Zahl n 0, so hat man den Bruch erweitert.
0, so hat man den Bruch erweitert.
Was ist eine Bruchzahl?
Definition Bruchzahl: eine Klasse von Brüchen, die durch Kürzen oder Erweitern auseinander hervorgehen.
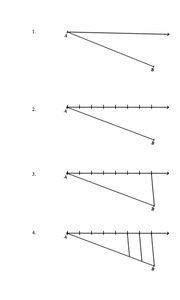
Konstruieren Sie nur mit Zirkel und Lineal  einer Strecke
einer Strecke 
Auf einer vom Punkt A ausgehenden Halbgeraden werden mit dem Zirkel 7 Punkte in gleichem Abstand abgetragen (2). Der hinterste Punkt wird mit B verbunden(3). Parallel zur entstandenen Strecke werden nun die weiteren Punkte auf der Halbgeraden mit der Strecke  verbunden, um die Strecke in Siebtel zu zerteilen (4) (Strahlensatz).
verbunden, um die Strecke in Siebtel zu zerteilen (4) (Strahlensatz).
_______
Ideen für eine Einführungsstunde
Idee 1 Pizza aufteilen
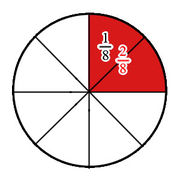
Bild 1
Die Idee ist, eine große Pizza in der Klasse zu zerteilen - mit dem Ziel, sie letztendlich zu essen. Letzteres soll der Motivation dienen. Wichtig ist, dass nicht nur zerteilt, also z.B. geachtelt wird, sondern dass auch auf Anteile wie  eigegangen wird (siehe Bild 1). Nur so ist ein wirkliches Verständnis von Brüchen möglich.
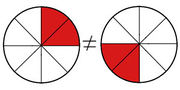
Außerdem muss beachtet werden, dass beim Pizza-Modell manche Schüler zwei Viertel eines Ganzen als unterschiedlich wahrnehmen (siehe Bild 2). Deshalb ist es unabdinglich, dass die Kinder konkret am Gegenstand arbeiten, statt nur Abbildungen zu nutzen, da das Verständnis so verbessert werden kann.
eigegangen wird (siehe Bild 1). Nur so ist ein wirkliches Verständnis von Brüchen möglich.
Außerdem muss beachtet werden, dass beim Pizza-Modell manche Schüler zwei Viertel eines Ganzen als unterschiedlich wahrnehmen (siehe Bild 2). Deshalb ist es unabdinglich, dass die Kinder konkret am Gegenstand arbeiten, statt nur Abbildungen zu nutzen, da das Verständnis so verbessert werden kann.
Bild 2
___________________
Das Ganze ist die Schulklasse, aufteilen der Schüler
Problem: Bei dieser Methode hat jeder Schüler nur einen lokalen Blick, während der globale Blick aufs Ganze fehlt. Um diesem Problem entgegenzuwirken, müsste man von oben auf die Klasse herabschauen (z.B. ein Foto machen).
Außerdem ist hier problematisch, dass die Schüler alle unterschiedlich sind (groß/klein etc.), aber alle den gleichen Anteil (z.B. 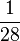 ) der Klasse repräsentieren sollen.
) der Klasse repräsentieren sollen.
bereits zerteilte Teile austeilen zusammensetzen
Die Idee besteht darin, dass schon vorbereitete Teile, z.B. Viertel und Drittel eines Kreises, von den Schülern zusammengefügt weden. Diese Idee eignet sich durchaus zur Vertiefung, ist allerdings als Einstieg ins Bruchrechnen eher ungeeigent. Grund ist, dass der Gedanke, dass eine Ausgangsmenge zerteilt wird, an den Schülern vorbeigeht. Dieser Gedanke ist für das Verständnis von Brüchen allerdings wesentlich.
Pizza vs. Blechkuchen
Vorteile Pizza
- Wie Uhr --> Anknüpfen an Vorwissen
- intuitiv
- man sieht gleich, wie viel fehlt
Nachteile Pizza
- schwierig für Brüche mit Nenner, die keine Zweierpotenzen sind (z.B.  )
)
- Zirkel benötigt
Vorteile Blechkuchen
- Für Flächenberechnungen einfacher
- Rechteck gut rasterbar
- Größe von Rechteck kann gut an Teile angepasst werden (z.B. 11cm breites Rechteck, wenn in Elftel geteilt werden soll)
Nachteile Blechkuchen
- Falten nicht immer eindeutig! Aber: Alle Lösungen müssen gewürdigt werden, was zeitintensiv ist
Beide Modelle haben ihre Vor- und Nachteile. Um vollständige Vorstellung von Brüchen zu entwickeln, müssen beide Modelle berücksichtigt werden!
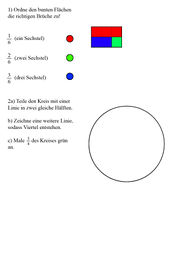
Arbeitsblätter zur Erstsicherung
Schreiben von Brüchen

Seite ergänzt von Stephan Grüner