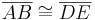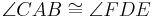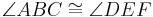Sätze
Aus Geometrie-Wiki
Version vom 8. Juli 2010, 08:36 Uhr von Rakorium (Diskussion | Beiträge)
Sätze
Satz I.1:
- Es seien g und h zwei Geraden. Wenn g und h nicht identisch sind, haben sie höchstens einen Punkt gemeinsam.
Satz I.2: (Kontraposition von Satz I.1)
- Es seien g und h zwei Geraden.
- Wenn g und h mehr als einen Punkt gemeinsam haben, so sind g und h identisch.
Satz I.3: (Existenz von drei Geraden)
- Es existieren mindestens drei paarweise verschiedene Geraden.
Satz I.5:
- Zwei voneinander verschiedene Ebenen haben entweder keinen Punkt oder eine Gerade gemeinsam, auf der alle gemeinsamen Punkte beider Ebenen liegen.
Satz I.6:
- Eine Ebene und eine nicht in ihr liegende Gerade haben höchstens einen Punkt gemeinsam.
Satz I.7:
- Jede Ebene enthält (wenigstens) drei Punkte.
Satz II.1:
- Aus
 folgt
folgt 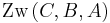 .
.
Satz II.2:
- Aus
 folgt
folgt 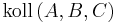 .
.
Satz II.3:
- Es sei
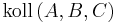 mit
mit 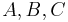 sind paarweise verschieden.
sind paarweise verschieden.
Dann gilt oder
oder 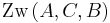 oder
oder  .
.
Satz II.4:
- Es sei
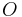 ein Punkt einer Geraden
ein Punkt einer Geraden  .
.
Die Teilmengen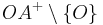 ,
, 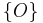 und
und 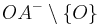 bilden eine Klasseneinteilung der Geraden
bilden eine Klasseneinteilung der Geraden  .
.
Satz III.1: (Existenz und Eindeutigkeit des Mittelpunkte einer Strecke)
- Jede Strecke hat genau einen Mittelpunkt.
Satz IV.1: (Repräsentantenunabhängigkeit)
- Wenn
 ein Punkt der Halbebene
ein Punkt der Halbebene 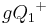 ist, dann gilt
ist, dann gilt 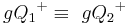 und
und  .
.
Satz IV.2:
- Halbebenen sind konvexe Punktmengen
Satz IV.3:
- Der Durchschnitt zweier konvexer Punktmengen ist konvex.
Satz V.1:
- Das Innere eines Winkels ist konvex.
Satz V.2:
- Wenn der Punkt
 im Inneren des Winkels
im Inneren des Winkels 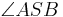 und nicht auf einem der Schenkel des Winkels
und nicht auf einem der Schenkel des Winkels 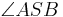 liegt, dann ist die Größe der beiden Teilwinkel
liegt, dann ist die Größe der beiden Teilwinkel 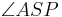 und
und  jeweils kleiner als die Größe des Winkels
jeweils kleiner als die Größe des Winkels 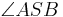 .
.
Satz V.3: (Existenz von rechten Winkeln)
- Es gibt rechte Winkel.
Satz V.4:
- Jeder rechte Winkel hat das Maß 90.
Satz V.5: ( Existenz und Eindeutigkeit der Senkrechten in einem Punkt)
- Gegeben seien ein Punkt P auf einer Geraden g in einer Ebene E. Es gibt in E genau eine Gerade, die durch P geht und senkrecht auf g steht.
oder
- Es sei
 eine Gerade der Ebene
eine Gerade der Ebene 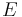 . Ferner sei
. Ferner sei  ein Punkt auf
ein Punkt auf  . In der Ebene
. In der Ebene 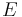 gibt es genau eine Gerade
gibt es genau eine Gerade 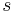 , die durch
, die durch  geht und senkrecht auf
geht und senkrecht auf  steht.
steht.
Satz VI.1: (Existenz und Eindeutigkeit der Mittelsenkrechten)
- Jede Strecke hat in jeder Ebene, zu der die Strecke vollständig gehört, genau eine Mittelsenkrechte.
Satz VI.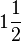 :
:
- Es sei
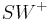 die Winkelhalbierende des Winkels
die Winkelhalbierende des Winkels 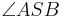 . Dann gilt
. Dann gilt 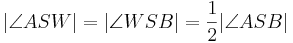 .
.
- Es sei
Satz VI.2: (Existenz und Eindeutigkeit der Winkelhalbierenden)
- Zu jedem Winkel gibt es genau eine Winkelhalbierende.
Satz VII.1:
- Die Relation kongruent ist auf der Menge aller Strecken eine Äquivalenzrelation.
Satz VII.2:
- Die Relation kongruent ist auf der Menge aller Winkel eine Äquivalenzrelation.
Satz VII.3:
- Die Relation kongruent ist auf der Menge aller Dreiecke eine Äquivalenzrelation.
Satz VII.4: (Kongruenzsatz WSW)
- Wenn für zwei Dreiecke
 und
und 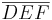 die folgenden 3 Kongruenzen
die folgenden 3 Kongruenzen
- Wenn für zwei Dreiecke
- gelten,
- dann sind die beiden Dreiecke
 und
und 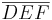 kongruent zueinander.
kongruent zueinander.
Satz VII.5: (Basiswinkelsatz)
- In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
Lemma 1:
- Die Winkelhalbierende
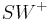 eines Winkels
eines Winkels 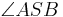 schneidet die Strecke
schneidet die Strecke 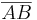 in genau einem Punkt
in genau einem Punkt  .
.
- Die Winkelhalbierende
Satz VII.6: (Mittelsenkrechtenkriterium)
- Eine Menge
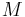 von Punkten ist genau dann die Mittelsenkrechte einer Strecke
von Punkten ist genau dann die Mittelsenkrechte einer Strecke  , wenn für jeden Punkt
, wenn für jeden Punkt 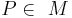 gilt:
gilt: 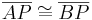 .
.
- Eine Menge
Satz VII.6 a: (hinreichende Bedingung dafür, dass ein Punkt zur Mittelsenkrechten von 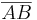 gehört.)
gehört.)
- Wenn ein Punkt
 zu den Endpunkten der Strecke
zu den Endpunkten der Strecke 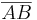 jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von
jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von 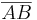 .
.
- Wenn ein Punkt
Satz VII.6 b: (notwendige Bedingung dafür, dass ein Punkt zur Mittelsenkrechten von 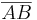 gehört)
gehört)
- Wenn ein Punkt
 zur Mittelsenkrechten der Strecke
zur Mittelsenkrechten der Strecke 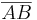 gehört, dann hat er zu den Punkten
gehört, dann hat er zu den Punkten 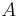 und
und 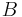 ein und denselben Abstand.
ein und denselben Abstand.
- Wenn ein Punkt
Satz VIII.1: (schwacher Außenwinkelsatz)
- Die Größe eines jeden Außenwinkels eines Dreiecks ist jeweils größer als die Größe eines jeden Innenwinkels dieses Dreiecks, der kein Nebenwinkel zu dem gewählten Außenwinkel des Dreiecks ist.
Lemma 2:
- Wenn ein Punkt
 im Inneren des Winkels
im Inneren des Winkels 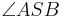 liegt, dann liegt der gesamte Strahl
liegt, dann liegt der gesamte Strahl 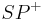 im Inneren des Winkels
im Inneren des Winkels 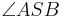 .
.
- Wenn ein Punkt