Übung Aufgaben 8 (SoSe 16)

Aufgabe 8.1

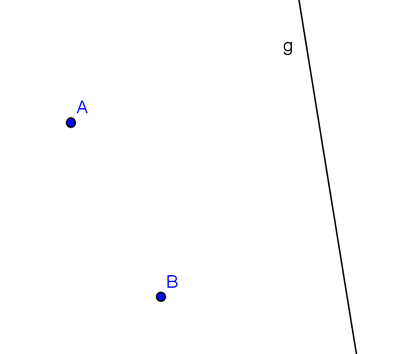
Das klassische Feuerwehrproblem: Am Punkt A steht die Feuerwehr, Punkt B symbolisiert das brennende Haus. Die Gerade g ist die Uferbegrenzung eines Flusses, aus dem die Feuerwehr das Wasser holen muss. Welchen Weg muss die Feuerwehr nehmen um Löschwasser am Fluss zu tanken um danach möglichst schnell am brennenden Haus zu sein? Konstruieren Sie nachstehend die optimale Route für die Feuerwehr und begründen Sie Ihre Konstruktion.
Das Problem lässt sich auf viele verschiedene Anwendungen übertragen, z. B.:

• reitende Cowboys, die ihr Pferd noch tränken müssen, bevor sie den Salon in Doce City erreichen
• Lichtstrahlen, die am Spiegel g reflektiert werden und immer den kürzesten Weg nehmen
• Billardkugeln, die durch einen zentralen Stoß und über Bande g einander treffen sollen
• ...

Lösung von Aufgabe 8.1P (SoSe_16)

Aufgabe 8.2

Wie hoch muss ein Spiegel sein, damit Sie sich ganz darin sehen können und auf welcher Höhe muss die Oberkante des Spiegels angebracht werden? Anmerkung: Sie dürfen hier die Strahlensätze, wie sie aus der Schule bekannt sind, verwenden. Tipp: Hier finden Sie eine hilfreiche GeoGebra-Applikation.

Lösung von Aufgabe 8.2P (SoSe_16)

Aufgabe 8.3

Die nachfolgende GeoGebra-Applikation zeigt einen Billardtisch mit zwei Kugeln in der Draufsicht. Kugel A soll durch einen zentralen Stoß die Kugel B über zwei Banden treffen. Konstruieren und Begründen Sie Ihre Konstruktion.

Lösung von Aufgabe 8.3P (SoSe_16)

Aufgabe 8.4

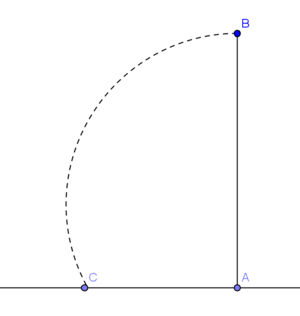
Auf einem neu anzulegenden Abenteuerspielplatz steht ein senkrecht nach oben ragender Baum (Strecke $\overline{AB}$ ). Dieser soll an einer Stelle K so angesägt werden, dass er hier umknickt und mit seiner Spitze an einer Stelle C am Boden zu liegen kommt (siehe Skizze). Konstruieren Sie die Knickstelle K.

Lösung von Aufgabe 8.4P (SoSe_16)