Lösung von Aufgabe 12.2
Aufgabenstellung
Beweisen Sie:
Korollar 1 zum schwachen Außenwinkelsatz
- In jedem Dreieck sind mindestens zwei Innenwinkel spitze Winkel.
Lösung 1
Definition spitzer Winkel: Ein spitzer Winkel ist kleiner als ein rechter Winkel. Definition korrekt? (Diskussion)
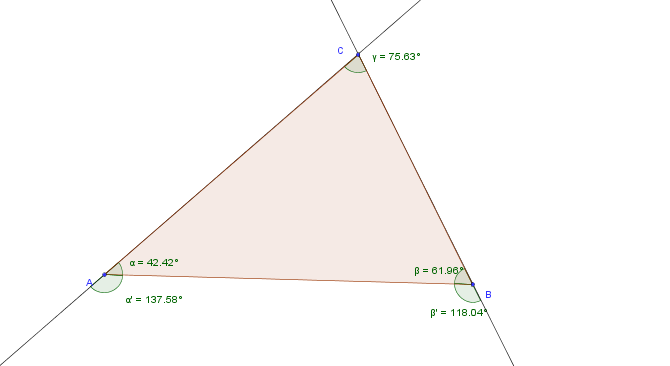
Voraussetzung: Dreieck 
Behauptung: o.B.d.A: 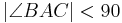 und
und 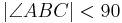
Der Einfachheit halber werden die Winkel mit 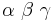 bezeichnet, die jeweiligen Außenwinkel sind dann
bezeichnet, die jeweiligen Außenwinkel sind dann 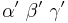
Behauptung:
- (1)
 und
und 
- oder (2)
 und
und 
- oder (3)
 und
und 
- (1)
Indirekter Beweis
- (1)
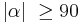 und
und 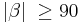
- oder (2)
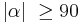 und
und 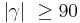
- oder (3)
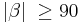 und
und 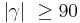
- (1)
Anmerkung: Man muss natürlich 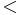 in der Behauptung durch
in der Behauptung durch 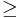 in der Annahme ersetzen, denn spitze Winkel sind KLEINER ALS rechte Winkel. Rechte Winkel selbst zählen somit nicht zur möglichen Menge. In der zu widerlegenden Annahme geht man somit von allen möglichen Fälle aus, also auch von dem Fall, dass zwei rechte Winkel in einem Dreieck möglich sind. Somit ist die Umkehrung des Korollars: "In jedem Dreieck gibt es höchstens einen rechten Winkel." Dies wird durch den Beweis gleich mit bewiesen! (Oder doch nicht? --> Diskussion)
in der Annahme ersetzen, denn spitze Winkel sind KLEINER ALS rechte Winkel. Rechte Winkel selbst zählen somit nicht zur möglichen Menge. In der zu widerlegenden Annahme geht man somit von allen möglichen Fälle aus, also auch von dem Fall, dass zwei rechte Winkel in einem Dreieck möglich sind. Somit ist die Umkehrung des Korollars: "In jedem Dreieck gibt es höchstens einen rechten Winkel." Dies wird durch den Beweis gleich mit bewiesen! (Oder doch nicht? --> Diskussion)
Annahme
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | Es gilt: 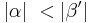 und und 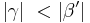
|
schwacher Außenwinkelsatz |
| (II) | 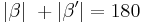
|
Axiom IV.4: (Supplementaxiom): Nebenwinkel sind supplementär. |
| (III) | 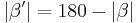
|
Algebraische Umformung |
| (IV) | ||
| (VI) | ||
| (VII) | ||
| (VIII) | ||
| (IX) | ||
| (X) |
--Heinzvaneugen 21:48, 11. Jul. 2010 (UTC)

