Linksinvers gleich Rechtsinvers
Satz 1
Es sei ![[G, \odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) eine Gruppe. eine Gruppe.
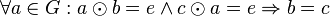
Beweis von Satz 1
Es sei 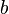 das Linksinverse bzgl. das Linksinverse bzgl. 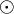 von von 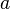 . .
Wir multiplizieren 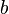 von rechts mit von rechts mit 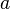 : :
| (I) |
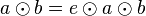 |
(Wir haben 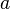 mit mit 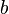 von rechts multipliziert von rechts multipliziert
|
| (II) |
 |
(Auch 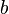 hat ein Linksinverses hat ein Linksinverses 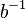
|
| (III) |
 |
(Assoziativität)
|
| (IV) |
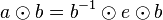 |
(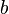 ist das Linksinverse von ist das Linksinverse von 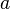 ) )
|
| (V) |
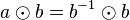 |
(Eigenschaften des Einselements)
|
| (VI) |
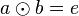 |
(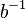 ist das Linksinverse von ist das Linksinverse von 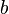
|
Mit Gleichung (VI) haben wir gezeigt, dass das Linksinverse von 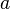 auch Rechtsinverses von auch Rechtsinverses von 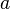 ist. ist.
Linkseins gleich Rechtseins
Satz 2
Es sei ![[G, \otimes]](/images/math/0/1/3/01322720752789c5d9651172aee2d990.png) eine Gruppe. Wenn eine Gruppe. Wenn  von links multipliziert Einselement von von links multipliziert Einselement von ![[G, \otimes]](/images/math/0/1/3/01322720752789c5d9651172aee2d990.png) ist, dann ist ist, dann ist  auch von rechts multipliziert Einselement von auch von rechts multipliziert Einselement von  . .
Beweis von Satz 2
Es sei ![[G, \otimes]](/images/math/0/1/3/01322720752789c5d9651172aee2d990.png) Gruppe. Es gelte ferner für das Element Gruppe. Es gelte ferner für das Element  die folgende Eigenschaft: die folgende Eigenschaft: 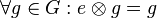 . .
Wir haben zu zeigen, dass jetzt auch 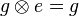 für alle für alle  aus aus  gilt. gilt.
| ![[G, \odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) eine Gruppe.
eine Gruppe.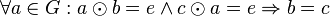
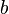 das Linksinverse bzgl.
das Linksinverse bzgl.  von
von 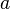 .
. 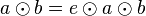

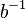

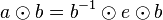
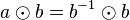
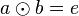
![[G, \otimes]](/images/math/0/1/3/01322720752789c5d9651172aee2d990.png) eine Gruppe. Wenn
eine Gruppe. Wenn  von links multipliziert Einselement von
von links multipliziert Einselement von  auch von rechts multipliziert Einselement von
auch von rechts multipliziert Einselement von  .
.
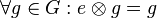 .
.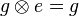 für alle
für alle  aus
aus 
