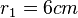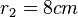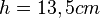Benutzer:SantaFe
Aus Geometrie-Wiki
Version vom 12. Dezember 2017, 11:10 Uhr von SantaFe (Diskussion | Beiträge)
Inhaltsverzeichnis |
Über mich
Sek 1 Mathematik Geographie
♥♣
Geometrie im Alltag
Blumentopf als Kegelstumpf
Volumen V eines Kegelstumpf
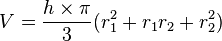
Wie viel Blumenerde passt in diesen Blumentopf?
In dem Fall dieses Blumentopf sind die Maße folgende:
Aus der Formel für das Volumen folgt somit:
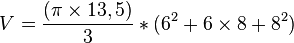
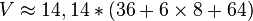
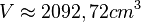
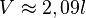
In den Blumetopf passen ca. 2,09 l Blumenerde.
| + | 0 | 1 | 2 | 3 |
| 0 | 0 | 1 | 2 | 3 |
| 1 | 1 | 2 | 3 | 0 |
| 2 | 2 | 3 | 0 | 1 |
| 3 | 3 | 0 | 1 | 2 |
Liebe Grüße an Lukas
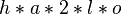
Links
Hallo SantaFe, ein tolles Beispiel hast du da gefunden ;)
Eine kleine Anmerkung: In der Tat handelt es sich bei einem Blumentopf um einen Kegelstumpf. Die Formel ist auch richtig. Jetzt wäre es schön Maße zu haben, um zu erfahren, wie viel Kubikcentimeter Erde in den Topf passen. Aber aufpassen! Nicht die Maße des äußeren Stumpfes nehmen, sondern um das Volumen zu berechnen, benötigen wir die Innenmaße, bzw. den inneren Kegelstumpf.
Gruß Alex
Hallo Tutor: Alex,
vielen Dank für die Rückmeldung. Die Seite wurde jetzt noch einmal bearbeitet.
Viele Grüße --SantaFe (Diskussion) 18:46, 27. Okt. 2016 (CEST)
Dank dir vielmals ;) --Tutor: Alex (Diskussion) 19:21, 27. Okt. 2016 (CEST)