Lösung von Aufgabe 10.1P (WS 17 18)
Aus Geometrie-Wiki
Version vom 15. Dezember 2017, 18:35 Uhr von Schnirch (Diskussion | Beiträge)
Beweisen Sie Satz IX.2:
Gegeben seien zwei Spiegelgeraden a und b mit einem gemeinsamen Schnittpunkt S, sowie zwei Punkten 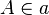 und
und 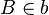 , die von S jeweils verschieden sind. Wir betrachten die Verkettung
, die von S jeweils verschieden sind. Wir betrachten die Verkettung  . Für einen beliebigen Punkt P und seinen Bildpunkt
. Für einen beliebigen Punkt P und seinen Bildpunkt  gilt:
gilt: 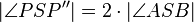 .
.

