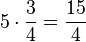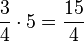Multiplikation von Bruchzahlen, Permanenzprinzip, Permanenzreihen, 09.06.2015
Inhaltsverzeichnis[Verbergen] |
Permanenzreihen
Multiplikation ganzer Zahlen
Wie muss die Reihe weitergehen?
-
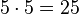
-
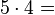
-
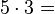
-
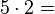
-
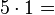
-
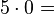
-
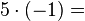
- ...
Um den Schülern die Rechenregel "minus mal minus gleich plus" näher zu bringen,führen wir die oben angefangene Permanenzreihe weiter und lassen die erste 5 kleiner werden.
-
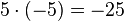
-
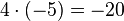
-
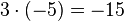
-
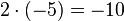
-
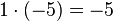
-
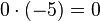
-
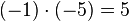
- ...
Wichtig ist die Zahlbereichserweiterung von den natürlichen Zahlen N zu den positiven rationalen Zahlen Q+. Wichtig ist außerdem, dass alle Gesetzmäßigkeiten aus N in Q+ auch gelten. --> Permanenzprinzip
Weiteres Beispiel für eine Permanenzreihe:
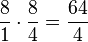
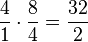
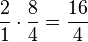
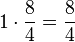
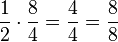
- ...
Bei 5. ist es mit den 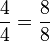 noch etwas ungeschickt. Daher sollte man sich für Schüler gegebenenfalls ein anderes Beispiel überlegen.
noch etwas ungeschickt. Daher sollte man sich für Schüler gegebenenfalls ein anderes Beispiel überlegen.
Alte Gesetzmäßigkeiten bleiben erhalten (Permanenzprinzip)
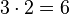
1.Beispiel
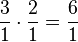
Schüler könnten hierbei auf die Idee kommen, dass die Rechenregel "bei gleichnamigen Brüchen: Nenner beibehalten und Zähler mal Zähler" lauten könnte. Dies sollte man die Schüler mithilfe eines weiteren Beispiel, einer Erweiterung des 1.Beispiels, überprüfen lassen.
Überprüfung:
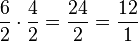
Anhand der Überprüfung lässt sich die Schüleridee verwerfen. Richtig wäre hier das Ergebnis 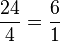 .
Eine weitere Schüleridee könnte es sein: "größerer Nenner beibehalten und Zähler mal Zähler". Auch diese Idee lässt sich durch eine Überprüfung mithilfe der erweiterten Beispielaufgabe verwerfen.
.
Eine weitere Schüleridee könnte es sein: "größerer Nenner beibehalten und Zähler mal Zähler". Auch diese Idee lässt sich durch eine Überprüfung mithilfe der erweiterten Beispielaufgabe verwerfen.
Überprüfung:
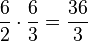
Gängige Prinzipien:
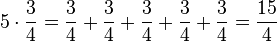
Wichtig ist hierbei, dass man mit den Schülern nicht mit dem Beispiel 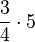 anfängt.
anfängt.
1. und 2. sind kommutativ. Aufgrund der Kommutativität der natürlichen Zahlen N sind auch die positiven rationalen Zahlen Q+ kommutativ.
Da dies im ersten Moment für Schüler sehr schwer zu verstehen ist, und man als Lehrer ungern sagt "das ist nun mal so, lernt es auswendig", kommt man an diesem Punkt der Mulitiplikation gemeiner Brüchen in den Bereich des Operatorkonzeptes (Von-Ansatz).
Beispiel:
 von
von 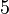 Um dies den Schülern näher zu bringen, ist es sinnvoll mit Skizzen (Kuchenblechmodell) zu arbeiten. Siehe Bilder.
Um dies den Schülern näher zu bringen, ist es sinnvoll mit Skizzen (Kuchenblechmodell) zu arbeiten. Siehe Bilder.