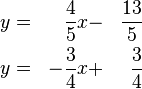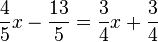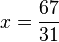analytische Geometrie SoSe 2018
Aus Geometrie-Wiki
Version vom 22. April 2018, 12:01 Uhr von *m.g.* (Diskussion | Beiträge)
|
Das Wiki für die Lehrveranstaltung "Lineare Algebra/analytische Geometrie", Sommersemester 2017
LiteraturAus früheren Semestern
Kapitel 1: Lineare GleichungssystemeLineare Gleichungssysteme mit zwei Variablen und zwei GleichungenLösungsmenge einer Gleichung mit zwei VariablenAllgemeine lineare Gleichung mit zwei Variablenax + by + c = 0
Grafische Veranschaulichung der Lösungsmenge einer Gleichung vom Typ ax+by=cEs seien
Das Gleichsetzungsverfahren
|
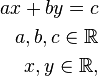
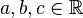 , beliebig aber fest,
, beliebig aber fest, 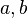 nicht gleichzeitig
nicht gleichzeitig 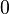 ,
,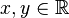 , variabel.
, variabel.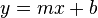 ,
, 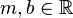 , beliebig aber fest,
, beliebig aber fest, 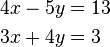
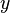 um:
um: