Allgemein
Wir betrachten die Implikation  . .
Die Implikation 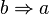 ist die Umkehrung der Implikation ist die Umkehrung der Implikation  . .
Wir vertauschen also die Rolle von Voraussetzung und Behauptung der Ausgangsimplikation.
Beide Implikationen, Ausgangsimplikation und zugehörige Umkehrung, müssen nicht zwangsläufig denselben Wahrheitsgehalt haben.
Beispiele
Beispiel 1
Implikation
Wenn eine Zahl 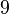 ein Teiler von ein Teiler von  ist, dann ist ist, dann ist  auch ein Teiler von auch ein Teiler von  . .
Voraussetzung: 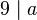
Behauptung: 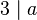
Die Implikation ist wahr, wie der folgende Beweis zeigt:
Wir übersetzten die Voraussetzung: 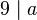
bedeutet: 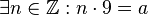 . .
Wir übersetzen die Behauptung: Fehler beim Parsen(Unbekannte Funktion „\mis“): 3 \mis a
bedeutet: 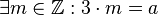 . .
|  .
.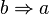 ist die Umkehrung der Implikation
ist die Umkehrung der Implikation 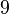 ein Teiler von
ein Teiler von  ist, dann ist
ist, dann ist  auch ein Teiler von
auch ein Teiler von 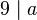
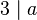
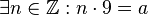 .
.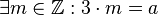 .
.
