Allgemein
Wir betrachten die Implikation  . .
Die Implikation 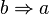 ist die Umkehrung der Implikation ist die Umkehrung der Implikation  . .
Wir vertauschen also die Rolle von Voraussetzung und Behauptung der Ausgangsimplikation.
Beide Implikationen, Ausgangsimplikation und zugehörige Umkehrung, müssen nicht zwangsläufig denselben Wahrheitsgehalt haben.
Beispiele
Beispiel 1: Teilbarkeit durch 3 und 9
Implikation: Aus der Teilbarkeit durch 9 folgt die Teilbarkeit durch 3
Wenn eine Zahl 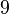 ein Teiler von ein Teiler von  ist, dann ist ist, dann ist  auch ein Teiler von auch ein Teiler von  . .
Voraussetzung: 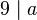
Behauptung: 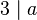
Die Implikation ist wahr, wie der folgende Beweis zeigt:
Wir übersetzten die Voraussetzung: 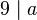
bedeutet: 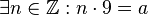 . .
Wir übersetzen die Behauptung: 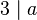 bedeutet: bedeutet: 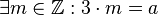 . .
Unter der Voraussetzung, dass eine ganze Zahl  existiert, die mit existiert, die mit 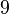 multipliziert multipliziert  ergibt,
müssen wir also zeigen, dass es eine ganze Zahl ergibt,
müssen wir also zeigen, dass es eine ganze Zahl  gibt, die mit gibt, die mit  multipliziert multipliziert  ergibt. ergibt.
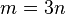 leistet das Verlangte: leistet das Verlangte:
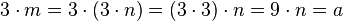 . .
Umkehrung: Aus der Teilbarkeit durch 3 folgt die Teilbarkeit durch 9
Wenn eine Zahl durch  teilbar ist, dann ist sie auch durch teilbar ist, dann ist sie auch durch 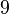 teilbar. teilbar.
Voraussetzung der Umkehrung: 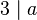
Behauptung der Umkehrung: 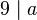
Die Umkehrung einer Implikation ist selbst wieder eine Implikation.
Die Aussage Wenn eine Zahl durch  teilbar ist, dann ist sie auch durch teilbar ist, dann ist sie auch durch 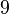 teilbar. ist wie die Implikation, aus der sie durch Umkehrung entstand, eine Allaussage: teilbar. ist wie die Implikation, aus der sie durch Umkehrung entstand, eine Allaussage:
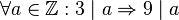
Nun gibt es ganze Zahlen wie etwa 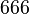 (the number of the biest), die sowohl durch (the number of the biest), die sowohl durch  als auch durch als auch durch 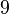 teilbar sind. Weil aber z.B. teilbar sind. Weil aber z.B. 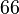 zwar durch zwar durch  , aber nicht durch , aber nicht durch 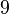 teilbar ist, muss die Umkehrung unserer Ausgangsimplikation keine wahre Aussage. teilbar ist, muss die Umkehrung unserer Ausgangsimplikation keine wahre Aussage.
Beispiel 2: In jedem Parallelogramm sind die gegenüberliegenden Seiten jeweils kongruent zueinander
Der Begriff Parallelogramm sei entsprechend der Semantik der Begriffsbezeichnung definiert:
- Jedes Viereck mit zwei Paaren paralleler Seiten ist ein Parallelogramm.
Implikation
Wenn ein Viereck ein Parallelogramm ist, dann sind seine gegenüberliegenden Seiten jeweils kongruent zueinander.
Beispiel 3: Jauch reloaded
Implikation: Jedes Rechteck ist ein Parallelogramm
Unter einem Rechteck wollen wir ein Viereck verstehen, dessen Diagonalen kongruent zueinander sind und die sich gegenseitig halbieren.
Ein Parallelogramm sei als Viereck definiert, dessen gegenüberliegende Seiten jeweils kongruent zueinander sind.
Unsere Implikation spezifiziert sich wie folgt:
- Wenn sich in einem Viereck die Diagonalen halbierend und zueinander kongruent sind, dann sind die gegenüberliegenden Seiten dieses Vierecks jeweils kongruent zueinander.
Voraussetzung
|  .
.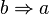 ist die Umkehrung der Implikation
ist die Umkehrung der Implikation 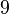 ein Teiler von
ein Teiler von  ist, dann ist
ist, dann ist  auch ein Teiler von
auch ein Teiler von 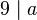
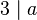
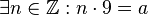 .
.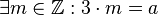 .
. existiert, die mit
existiert, die mit  gibt, die mit
gibt, die mit 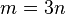 leistet das Verlangte:
leistet das Verlangte: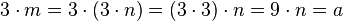 .
.
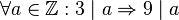
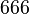 (
(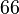 zwar durch
zwar durch 
