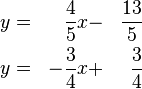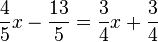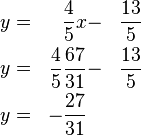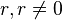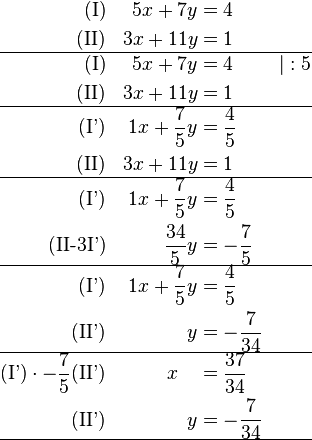analytische Geometrie SoSe 2018
Aus Geometrie-Wiki
Version vom 3. Mai 2018, 15:18 Uhr von *m.g.* (Diskussion | Beiträge)
|
Das Wiki für die Lehrveranstaltung "Lineare Algebra/analytische Geometrie", Sommersemester 2017
LiteraturAus früheren Semestern
Kapitel 1: Lineare GleichungssystemeLineare Gleichungssysteme mit zwei Variablen und zwei GleichungenAllgemeine lineare Gleichung mit zwei Variablen
Lösen eines linearen Gleichungssystems mit zwei Gleichungen und zwei UnbekanntenDas Gleichsetzungsverfahren
[ www.geogebra.org is not an authorized iframe site ]
Das AdditionsverfahrenÄquivalenzumformungen für Lineare Gleichungssysteme
Beispiel 1
Lösbarkeit eines Linearen Gleichungssystems mit zwei Gleichungen und zwei Unbekannten |
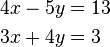
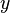 um:
um: