Übungsaufgaben zur Algebra, Serie 3 SoSe 2018
Aus Geometrie-Wiki
Version vom 5. Mai 2018, 14:47 Uhr von *m.g.* (Diskussion | Beiträge)
Aufgabe 3.1Es seien Aufgabe 3.2Aufgabe 3.3Aufgabe 3.4Aufgabe 3.5Aufgabe 3.6Aufgabe 3.7Aufgabe 3.8Aufgabe 3.9Aufgabe 3.10 |
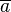 und
und 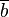 zwei Restklassen bzgl. des selben Moduls
zwei Restklassen bzgl. des selben Moduls  . Beweisen Sie die Repräsentantenunabhängigkeit Restklassenaddition:
. Beweisen Sie die Repräsentantenunabhängigkeit Restklassenaddition: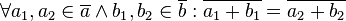 .
.

