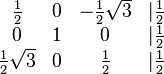Serie 3: LGS lösen SoSe 2018

Aufgabe 3.1 SoSe 2018 Lösen Sie das folgende Gleichungssystem: $\begin{pmatrix} \frac{1}{2}\sqrt{2} & - \frac{1}{2}\sqrt{2} \\ \frac{1}{2}\sqrt{2} & \frac{1}{2}\sqrt{2} \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \end{pmatrix}$. Aufgabe 3.2 SoSe 2018 Lösen Sie das folgende Gleichungssystem: $\begin{pmatrix} \frac{1}{2}\sqrt{3} & - \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2}\sqrt{3} \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \end{pmatrix}$. Aufgabe 3.3 Gegeben ist die große Koeffizientenmatrix eines lineraren Gleichungssystems: $\begin{matrix} \frac{1}{2} & 0 & -\frac{1}{2}\sqrt{3} & \vert \frac{1}{2} \\ 0 & 1 & 0 & \vert \frac{1}{2} \\ \frac{1}{2}\sqrt{3} & 0 & \frac{1}{2} & \vert \frac{1}{2} \end{matrix}$ Lösen Sie dieses Gleichungssystem. Aufgabe 3.4
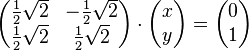
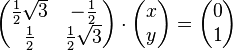