Serie 4: größere LSG lösen SoSe 2018
Aufgabe 4.1 SoSe 2018Es seien
Aufgabe 4.2 SoSe 2018Geben Sie ein lineares Gleichungssystem vom Typ Aufgabe 4.3 SoSe 2018Beschreiben Sie die Gerade Aufgabe 4.5 SoSe 2018Lösen Sie das folgende LGS, indem Sie es auf Diagonalenform bringen: Aufgabe 4.6 SoSe 2018Lösen Sie das folgende LGS, indem Sie es auf Diagonalenform bringen: Aufgabe 4.7 SoSe 2018Gegeben seien die folgenden Punkte Wir betrachten einen Würfel mit den Eckpunkten (a) Beschreiben Sie die Flächen dieses Würfels mittels Gleichungen vom Typ Aufgabe 4.8 SoSe 2018Aufgabe 4.9 SoSe 2018Aufgabe 4.10 SoSe 2018 |
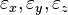 drei Ebenen im
drei Ebenen im 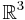 , die genau den Punkt
, die genau den Punkt 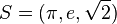 gemeinsam haben.
gemeinsam haben.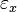 ist parallel zur
ist parallel zur 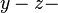 Ebene,
Ebene,
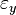 ist parallel zur
ist parallel zur 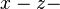 Ebene,
Ebene,
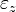 ist parallel zur
ist parallel zur 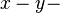 Ebene.
Ebene.
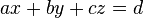 .
.
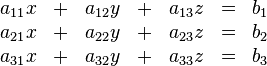
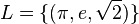 hat.
hat.
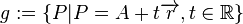 für
für 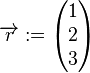 und
und 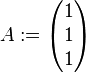 als Lösungsmenge eines Gleichungssystems vom Typ
als Lösungsmenge eines Gleichungssystems vom Typ 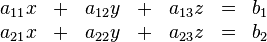 .
.
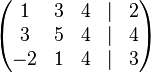
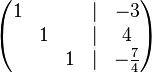
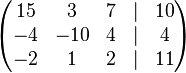
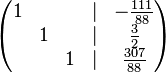
 :
: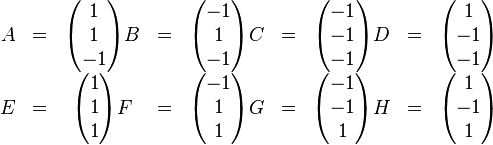
 .
.
