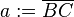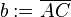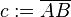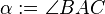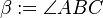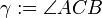Lösung Aufgabe 2.3 SoSe 2018

Aufgabe 2.3 SoSe 2018

Formulieren Sie den Basiswinkelsatz für Dreiecke in Wenn-Dann-Form und beweisen Sie ihn. Verwenden Sie für den Beweis die Existenz der Winkelhalbierenden eines Winkels und den Kongruenzsatz SWS. Beziehen Sie sich in Ihrem Beweis sinnvollerweise auf eine Skizze.

Lösung

Basiswinkelsatz in "Wenn-Dann"

Wenn Ein Dreieck gleichschenklig ist, dann sind seine Basiswinkel kongruent zueinander.

Beweis

Es sei $\overline{ABC}$ ein Dreieck mit den schulüblichen Bezeichnungen:

• $a:=\overline{BC}$
• $b:=\overline{AC}$
• $c:=\overline{AB}$
• $\alpha := \angle BAC$
• $\beta := \angle ABC$
• $\gamma := \angle ACB$