Aufgabe 2.6 SoSe 2018
Wir setzen den Innenwinkelsatz für Dreiecke und den Nebenwinkelsatz als bewiesen voraus.
Satz: (starker Außenwinkelsatz)
- Jeder Außenwinkel eines Dreiecks ist so groß wie die Summe der Größen der beiden nicht anliegenden Innenwinkel.
a) Formulieren Sie den starken Außenwinkelatz in Wenn-Dann-Form.
b) Formulieren Sie die Voraussetzung und die Behauptung des starken Außenwinkelsatzes unter Verwendung der Bezeichnungen in der folgenden Skizze:
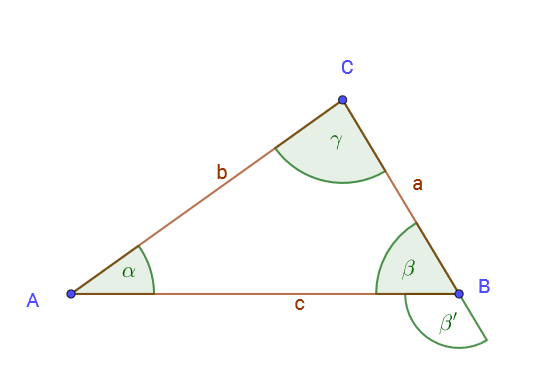
c) Beweisen Sie den starken Außenwinkelsatz.
Lösung
Teilaufgabe a)
Wenn ein Winkel 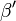 ein Außenwinkel eines Dreiecks ein Außenwinkel eines Dreiecks 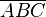 ist, dann ist seine Größe gleich der Summe der Größen der beiden Innenwinkel von ist, dann ist seine Größe gleich der Summe der Größen der beiden Innenwinkel von 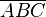 , die keine Nebenwinkel zu , die keine Nebenwinkel zu 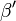 sind. sind.
Teilaufgabe b)
Voraussetzung
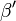 ist Außenwinkel von ist Außenwinkel von 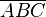 . .
Behauptung
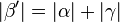
|