Serie 2: Zwei Gleichungen mit zwei Unbekannten SoSe 2018
Aufgabe 2.1 SoSe 2018Gegeben Sei das Gleichungssystem Aufgabe 2.2 SoSe 2018Gegeben sind die kleinen Koeffizientenmatrizen:
a) In welchem Fall könnte das zugehörige Gleichungssystem eindeutig lösbar sein? Aufgabe 2.3 SoSe 2018Gegeben sei die Matrix Aufgabe 2.4 SoSe 2018Gegeben Sei das Gleichungssystem Aufgabe 2.5 SoSe 2018Lösen Sie das folgende LGS. Geben Sie die Lösungsmenge in Form gemeiner Brüche an.
Aufgabe 2.6 SoSe 2018Entwerfen Sie für die Klassenstufe 9 eine Sachrechenaufgabe im Kontext "Handytarife", deren Lösung auf ein LGS mit zwei Gleichungen und zwei Unbekannten führt. |
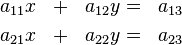 .
. 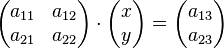 ist.
ist.
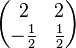

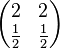
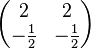
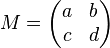 .
. 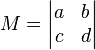 von
von  berechnet sich zu
berechnet sich zu 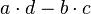 .
. 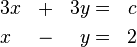 .
. .
.