Lösung von Aufgabe 8.6
Definieren Sie die Begriffe Stufenwinkel und Wechselwinkel (an geschnittenen Geraden).
Lösung--Schnirch 11:31, 15. Jul. 2010 (UTC)
Definition (Stufenwinkel): Zwei Winkel 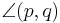 und
und 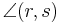 heißen Stufenwinkel, falls ein Schenkel
heißen Stufenwinkel, falls ein Schenkel 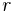 des einen Winkels Teilmenge eines Schenkels
des einen Winkels Teilmenge eines Schenkels  des anderen Winkels ist und die anderen beiden Schenkel
des anderen Winkels ist und die anderen beiden Schenkel 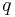 und
und 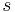 in einer Halbebene bezüglich der Geraden
in einer Halbebene bezüglich der Geraden  liegen, die durch die beiden Schenkel
liegen, die durch die beiden Schenkel  und
und 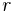 gegeben ist.
gegeben ist.
Definition (Wechselwinkel): Zwei Winkel 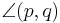 und
und 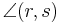 heißen Wechselwinkel, falls der Scheitelwinkel des Winkels
heißen Wechselwinkel, falls der Scheitelwinkel des Winkels 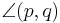 und der Winkel
und der Winkel 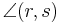 Stufenwinkel sind.
Stufenwinkel sind.
vorangegangene Diskussion
Es seien g und h zwei verschiedene Geraden.
Werden g und h von einer weiteren Geraden i geschnitten, so heißen zwei innere oder zwei äußere Winkel auf verschiedenen Seiten der schneidenden Gerade i, die nicht Nebenwinkel sind, Wechselwinkel.
Stufenwinkel heißen ein innerer und ein äußerer Winkel auf der selben Seite der schneidenden Gerade i, die nicht Nebenwinkel sind.
--Maude001 17:36, 19. Jun. 2010 (UTC)
Noch ein Vorschlag für Stufenwinkel:
Würde man g auf h abbilden, so sind die Winkel Stufenwinkel, die auf diese Weise aufeinander liegen würden.--Nicola 17:19, 24. Jun. 2010 (UTC)

