Lösung von Aufg. 6.3P (WS 18 19)

Beweisen Sie: Der Durchschnitt zweier konvexer Punktmengen ist konvex.

1. M ∩ N = O, mit M, N, O sind konvex
2. {A,B | $\overline{AB}$ ε M} ∩ {C,D | $\overline{CD}$ ε M} <=> O
3. O = {A,B,C,D | $\overline{AB}$ ε M $\wedge$ $\overline{AB}$ ε N $\wedge$ $\overline{CD}$ ε M $\wedge$ $\overline{CD}$ ε N}
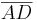
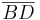
4. O = {A,B,C,D | $\overline{AB}$ $\wedge$ $\overline{AC}$ $\wedge$ $\overline{AD}$ $\wedge$ $\overline{BC}$ $\wedge$ $\overline{BD}$ $\wedge$ $\overline{CD}$ ε O}
5. O ist konvex.