Lösung von Aufg. 7.3P (WS 18 19)
Gegeben seien drei paarweise verschiedene und kollineare Punkte A, B und C in einer Ebene E. Ferner sei eine Gerade g Teilmenge der Ebene E, wobei keiner der Punkte A, B und C auf g liegen möge. Beweisen Sie folgenden Zusammenhang:
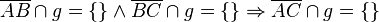
(Hinweis: Nehmen Sie einen weiteren Punkt D an, mit 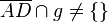 und nutzen Sie den Satz von Pasch)
und nutzen Sie den Satz von Pasch)
Die Punkte A, B, D bilden das Dreieck 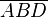 ,
,  wird von g nicht geschnitten,
wird von g nicht geschnitten, 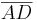 wird geschnitten. - Voraussetzung, Hinweis
wird geschnitten. - Voraussetzung, Hinweis
=> g muss noch eine weitere Seite von 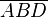 schneiden, also
schneiden, also 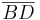 . - 1., Satz von Pasch
. - 1., Satz von Pasch
=> B, C, D bilden ein Dreieck 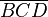 , g schneidet
, g schneidet 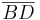 und genau eine weitere Seite. - Satz von Pasch
und genau eine weitere Seite. - Satz von Pasch
=> g schneidet  , da g
, da g  nicht schneidet. - 3., Vorraussetzung
nicht schneidet. - 3., Vorraussetzung
=> A, C, D bilden das Dreieck  , g schneidet
, g schneidet 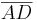 und
und 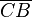 , somit kann g
, somit kann g  nicht schneiden. - 1., 4., Satz von Pasch--CIG UA (Diskussion) 15:24, 30. Nov. 2018 (CET)
nicht schneiden. - 1., 4., Satz von Pasch--CIG UA (Diskussion) 15:24, 30. Nov. 2018 (CET)

