Lösung von Zusatzaufg. 7.2P (WS 18 19)

Beweisen Sie: Halbebenen sind konvexe Punktmengen.

Eine Halbebene 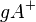$gA^+$ ist die Menge aller Punkte P (und A), für die gilt, dass 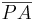$\overline{PA}$ g nicht schneidet, also steht P in Relation zu A (PRA). - Def(Halbebene)
=> P1RA $\wedge$ P2RA => P1RP2. - Symmetrie der Relation
=> Da alle Punkte der Halbebene in Relation zu A stehen, stehen sie auch untereinander in Relation. Somit ist 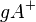$gA^+$ eine konvexe Punktmenge.--CIG UA (Diskussion) 16:11, 30. Nov. 2018 (CET)