19)
Aus Geometrie-Wiki
Version vom 20. Dezember 2018, 22:12 Uhr von CIG UA (Diskussion | Beiträge)
Beweisen Sie Satz IX.3:
Bei einer Punktspiegelung ist der Schnittpunkt S der beiden Spiegelgeraden a und b Mittelpunkt der Strecke 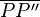 , mit
, mit 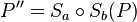 .
.
Vor: P = Sa  Sb (P) und
Sb (P) und 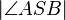 = 90° mit A ε a und B ε b; Beh: |PS| = |SP| mit S ε PP
= 90° mit A ε a und B ε b; Beh: |PS| = |SP| mit S ε PP
1.) Sa (P) = P' und Sb (P') = 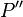 - Vor., Verkettung von Geradenspiegelungen
- Vor., Verkettung von Geradenspiegelungen
2.) 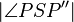 = 2
= 2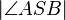 - 1.), Beweis aus 10.2
- 1.), Beweis aus 10.2
3.) 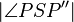 = 2 × 90° = 180° - Vor., 2.)
= 2 × 90° = 180° - Vor., 2.)
4.) 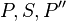 sind kollinear => S ε PP - 3.)
sind kollinear => S ε PP - 3.)
5.) |PS| = |P'S| und |P'S| = 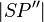 - 1.), Längenerhaltung
- 1.), Längenerhaltung
6. |PS| = 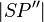 - 5.)
- 5.)
7.) Zw (P,S,P) - 4.), 6.), Zwischenrelation
=> S liegt auf 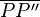 und ist von beiden Endpunkten gleich weit entfernt, die Behauptung ist bewiesen.--CIG UA (Diskussion) 22:12, 20. Dez. 2018 (CET)
und ist von beiden Endpunkten gleich weit entfernt, die Behauptung ist bewiesen.--CIG UA (Diskussion) 22:12, 20. Dez. 2018 (CET)

