Diskussion:Beziehungen zwischen den Seitenlängen und den Innenwinkelgrößen eines Dreiecks
Aus Geometrie-Wiki
Version vom 17. Juli 2010, 14:55 Uhr von Maude001 (Diskussion | Beiträge)
Umkehrung des Satzes:
Der größte Innenwinkel eines Dreiecks liegt der längsten Seite des Dreiecks gegenüber.
Der kleinste Innenwinkel eines Dreiecks liegt die kürzesten Seite des Dreiecks gegenüber.
--Mirasol 07:54, 6. Jul. 2010 (UTC)
Was bisher geschah: --*m.g.* 04:09, 15. Jul. 2010 (UTC)
Satz:
Der längsten Seite eines Dreiecks liegt der größte Innenwinkel des Dreiecks gegenüber.
Ebenso gilt:
Der kürzesten Seite eines Dreiecks liegt der kleinste Innenwinkel des Dreiecks gegenüber.
Kommentar --*m.g.* 21:12, 5. Jul. 2010 (UTC):
Super! Jetzt noch die Umkehrung?
Dem größten Innenwinkel eines Dreiecks liegt die längste Seite gegenüber.
Dem kleinsten Innenwinkel eines Dreiecks liegt die kürzeste Seite gegenüber.
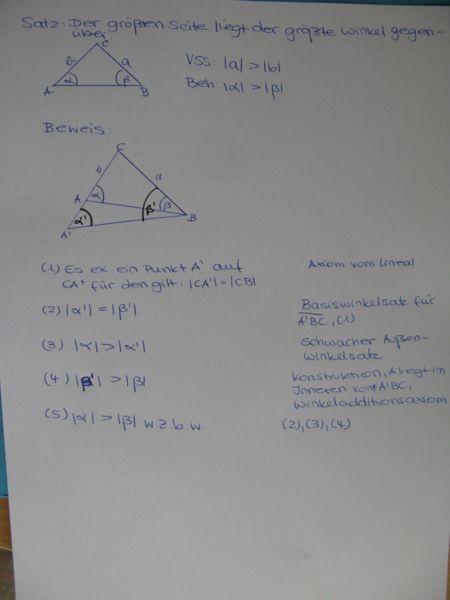
Satz IX.2: (Der größeren Seite liegt der größere Winkel gegenüber)
- Es sei
 ein Dreieck mit den schulüblichen Bezeichnungen.
ein Dreieck mit den schulüblichen Bezeichnungen.
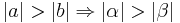
- Es sei
Der Beweis noch andersrum: