GeometrieUndUnterrichtSS2019 12

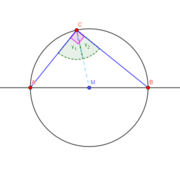
Der Satz des Thales und formaler Beweis

Mögliche Formulierung: „Alle Winkel an einem Halbkreis sind rechte Winkel“.

Skizze zur Veranschalichung des Beweises (Thales)

Formaler Beweis

Es ist 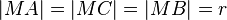$|MA| = |MC| = |MB| = r$, wobei r den Radius des Kreises bezeichnet. Demnach sind ΔAMC und ΔMBC gleichschenklig.

Insbesonders gilt aufgrund des Basiswinkelsatzes für gleichschenklige Dreiecke: 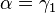$\alpha = \gamma_1$ und $\beta = \gamma_2$.

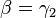Wegen des Satzes der Winkelsumme im Dreieck ΔABC gilt:

$\alpha + \beta + (\gamma_1 + \gamma_2) = 180^\circ$,

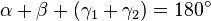und mit 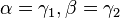$\alpha = \gamma_1 , \beta = \gamma_2$ ergibt sich

$2( \gamma_1 + \gamma_2 ) = 180^\circ -> \gamma = \gamma_1 + \gamma_2 = 90^\circ$.

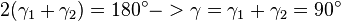Vorüberlegungen

Bereitstellung und/oder Aktivierung von Vorwissen der Schülerinnen und Schüler

Zunächst stellte sich die Frage, welches Vorwissen bei den SuS vorhanden sein und aktiviert werden muss. Dies wurde an der Tafel zusammengetragen:

• Alle Punkte auf einer Kreislinie haben den gleichen Abstand zum Kreismittelpunkt
• Basiswinkelsatz für gleichschenklige Dreiecke
• Satz über Winkelsumme im Dreieck, Rechnen mit Winkeln (Addierbarkeit, Ergänzung von Winkeln)
• Lösungsverfahren von Gleichungen, speziell Einsetzungsverfahren
• Definition & Eigenschaften von gleichschenkligen Dreiecken

Anschließend wurde diskutiert, wie man dieses Vorwissen aktivieren könne, im Hinblick auf den möglichen Zeitaufwand zu Beginn einer Unterrichtsstunde. Genannt wurden Besprechung von Hausaufgaben, Kurzteste oder -abfragen sowie ein Quizz zu beginn. Für letzteres sollten Fragen entworfen werden, die im Idealfall aus Zeitgründen kompakt, aber dennoch alles abdecken sollten. Beispiele waren:

• Was ist ein Kreis?
• Was ist ein (gleichschenkliges) Dreieck?
• Wieviele rechte Winkel kann ein Dreieck haben?

Allerdings wurden auf den Einwand hin, dass eventuell Schwierigkeiten dabei auftreten könnten, den Bezug dieses Wissen zum Beweis zu sehen, noch bildliche Beispiele genannt, die in Richtung der obigen Skizze des Beweises gingen. Hierbei könnte man fragen: "Wie lang ist |AB|?" usw.

Kollaborative Unterrichtsskizze zur Beweisaufgabe: „Satz des Thales“

Aktivierung von Vorwissen

Ergebnis (Arbeitsblatt) zum Arbeitsauftrag: „Aktivieren von Vorwissen für den Satz des Thales“

Entdecken und Formulieren vom Satz des Thales

Ergebnis (Arbeitsblatt) zum Arbeitsauftrag: „Entdecken und Erarbeiten der Aussage vom Satz des Thales“

Exploration der Phänomensituation (Thalesfiguren)

Ergebnis (Arbeitsblatt) zum Arbeitsauftrag: „Exploration von Thalesfiguren“

Beweisfindung und Argumentation

Ergebnis (Arbeitsblatt) zum Arbeitsauftrag: „Beweisfindung und Argumentieren zum Satz des Thales“