Lösung von Aufgabe 7.10
Beweisen Sie: Jede Strecke hat höchstens einen Mittelpunkt.
Die Lösung von Maude001 ist korrekt - super! --Schnirch 09:57, 8. Jul. 2010 (UTC)
A--M--B
Voraussetzung: koll(A, M, B), zw (A, M, B), 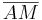 =
= 
- (gemeint ist:
 ) --Sternchen 13:25, 10. Jun. 2010 (UTC)
) --Sternchen 13:25, 10. Jun. 2010 (UTC)
zu zeigen: Es gibt nur einen Punkt M, auf den die o.g. Sachverhalte zutreffen.
M = Mittelpunkt, da Definition III.1: (Mittelpunkt einer Strecke)
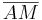 ist eindeutig für
ist eindeutig für  definiert
Axiom II.1: (Abstandsaxiom)
definiert
Axiom II.1: (Abstandsaxiom)
--Nicola 13:52, 6. Jun. 2010 (UTC)
noch ein Versuch:
Satz III.1: Jede Strecke hat einen und nur einen Mittelpunkt.
1. Existenzbeweis bereits in der Vorlesung geführt.
2. Eindeutigkeitsbeweis: Jede Strecke hat höchstens einen Mittelpunkt.
Annahme: Es existieren zwei verschiedene Mittelpunkte 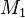 und
und  , die Element von
, die Element von  sind.
sind.
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 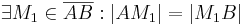 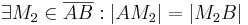
|
Annahme |
| (II) | 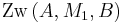 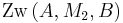
|
(I), Existenzbeweis, Def. (zw) |
| (III) | 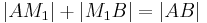 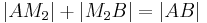
|
Def (zw), (II) |
| (IV) | 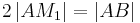 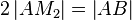
|
(I), (III), Rechnen in 
|
| (V) | 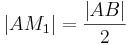 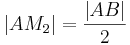
|
Rechnen in  , (IV) , (IV)
|
| (VI) | 
|
(V), Rechnen in 
|
| (VII) | 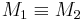 Widerspruch zur Annahme 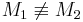 Es existiert höchstens ein Mittelpunkt der Strecke  . .
|
(VI) |
--Maude001 13:16, 20. Jun. 2010 (UTC)
Mal eine generelle Frage:
Ist der Existenzbeweis im Falle des Mittelpunktes nicht schon ausreichend für die Eindeutigkeit des Mittelpunktes? Denn das Axiom II.1 und das Axiom vom Lineal, die für den Existenzbeweis verwendet wurden, machen ja schon eindeutige Aussagen.
Bei den Aufgaben Übung 7.1 und 7.2 war zumindest ein Beweis ausreichend. --Barbarossa 15:34, 19. Jul. 2010 (UTC)

