GeometrieUndUnterrichtSS2019 12
Der Satz des Thales und formaler Beweis
Mögliche Formulierung: „Alle Winkel an einem Halbkreis sind rechte Winkel“.
Formaler Beweis
Es ist 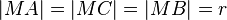 ,
wobei r den Radius des Kreises bezeichnet. Demnach sind ΔAMC und ΔMBC gleichschenklig.
,
wobei r den Radius des Kreises bezeichnet. Demnach sind ΔAMC und ΔMBC gleichschenklig.
Insbesonders gilt aufgrund des Basiswinkelsatzes für gleichschenklige Dreiecke: 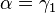 und
und 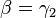 .
.
Wegen des Satzes der Winkelsumme im Dreieck ΔABC gilt:
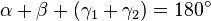 ,
,
und mit 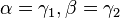 ergibt sich
ergibt sich
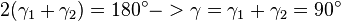 .
.
Vorüberlegungen
In Anknüpfung an die vorherige Sitzung zum Thema "Beweisen und Argumentieren" werden die idealtypischen Bestandteile von Beweisprozessen in der Schule wiederholt. Da das Ziel der Sitzung ist, in gemeinsamer Arbeit eine mögliche Unterrichtsskizze zum Thema "Beweis vom Satz des Thales" zu entwerfen, werden die Bestandteile hier auf das Beispiel "Beweis vom Satz des Thales" bezogen.
Bereitstellung und/oder Aktivierung von Vorwissen der Schülerinnen und Schüler
Zunächst stellt sich die Frage, welches Vorwissen bei den SuS vorhanden sein und deswegen zu Beginn der geplanten Unterrichtsstunde aktiviert werden muss, damit dieses zum Beweisen des Satzes benutzt werden kann. Die nötigen Fakten wurden bereits in der vorherigen Sitzung an der Tafel zusammengetragen:
- Alle Punkte auf einer Kreislinie haben den gleichen Abstand zum Kreismittelpunkt.
- Basiswinkelsatz für gleichschenklige Dreiecke
- Satz über Winkelsumme im Dreieck, Rechnen mit Winkeln (Addierbarkeit, Ergänzung von Winkeln)
- Lösungsverfahren von Gleichungen, speziell Einsetzungsverfahren
- Definition & Eigenschaften von gleichschenkligen Dreiecken
Da es sich bei diesem Bestandteil des Beweisprozesses nur um die Vorarbeit für die eigentliche Beweisarbeit handelt, sollte die Phase der Aktivierung von Vorwissen entsprechend nicht zu viel Unterrichtszeit in Anspruch nehmen. Mögliche Methoden wären beispielsweise die Durchführung eines Quizzes im Plenum, oder das Bearbeiten eines Arbeitsblattes in Einzelarbeit. Inhaltlich sollen die gestellten Aufgaben logischerweise auf das benötigte Vorwissen abzielen.
Finden und Formulieren der Vermutung (zum Satz des Thales)
Dieser Bestandteil zielt zunächst auf die Exploration und eine intensive Auseinandersetzung mit der Problemstellung ab, um die SuS für diese zu sensibilisieren. Dabei können von den SuS Gesetzmäßigkeiten identifiziert oder bereits Bedingungen erkannt werden, die Voraussetzung für diese Gesetzmäßigkeit sind. Entsprechende Hypothesen werden aufgestellt. Diese Phase ist eher von einer empirischer Arbeitsweise geprägt.
Explorieren oder Operatives Durcharbeiten der Problemsituation
Indem Bedingungen der Problemstellung variiert und die Auswirkungen dieser Änderungen untersucht werden, sollen SuS die Hypothese bzw. Vermutung des vorangegangenen Schrittes überprüfen: "Gilt die Vermutung auch bei veränderten Bedingungen? Welche Bedingungen oder Voraussetzungen sind wirklich erforderlich?"
Darüber hinaus erhalten sie Einsichten über Spezialfälle, Einschränkungen oder Möglichkeiten der Verallgemeinerung der Vermutung.
Beweisfindung und inhaltlich-anschauliche Argumente
Nachdem die SuS erarbeitet haben, welche Bedingungen/Voraussetzungen der Problemstellung relevant für die zu beweisende Aussage sind, müssen sie Argumente für deren Gültigkeit sammeln. Diese müssen noch nicht formalisiert festgehalten werden, sondern können auch inhaltlich-anschaulicher Art sein. Wesentlich ist in dieser Phase auch die Verknüpfung der Argumente zu einer kohärenten und logischen Argumentationskette.
Formalisierung der Beweisargumentation
Diese Phase dient dazu, die bereits aufgestellte Argumentationskette zu formalisieren, d.h. den Beweis in "die Sprache der Mathematik zu übersetzen". Die Formalisierung des Beweises spielt im Mathematikunterricht jedoch meist eine eher untergeordnete Rolle und soll deshalb auch in der geplanten Unterrichtsstunde zum Beweis vom Satz des Thales vernachlässigt werden.
Rückschau, operatives Durcharbeiten des Beweises
Dieser Bestandteil ähnelt stark dem "Explorieren oder Operativen Durcharbeiten der Problemsituation". Nachdem der Beweisprozess an sich abgeschlossen ist, handelt es sich bei dieser Phase um eine Art Rückschau, die der Überprüfung des Beweises dienen soll: "Sind die aufgestellten Voraussetzungen wirklich nötig? Welche Auswirkung hat das Weglassen einer Bedingung?"
Kollaborative Unterrichtsskizze zur Beweisaufgabe: „Satz des Thales“
Aktivierung von Vorwissen
Zur Vorbereitung des Beweises zum Satz des Thales sollten die benötigten Regeln und Sätze in möglichst kurzer Zeit wiederholt werden. Als geeignete Methode ergab sich die Bearbeitung eines Arbeitsblattes mit vier Aufgaben in Einzelarbeit, um zu gewährleisten, dass jeder einzelne Schüler/jede einzelne Schülerin sich mit den Inhalten beschäftigt.
Die konkrete Abfrage von Sätzen oder Definitionen erschien zur Vorbereitung des Beweises wenig sinnvoll, da beim Beweisen deren Anwendung erforderlich ist. Um die Problemstellungen zu verdeutlichen und Bezüge zur Problemstellung vom Satz des Thales herzustellen, sollten die SuS mit möglichst vielen Skizzen arbeiten. Mit dem Ziel, die SuS für das Transparentmachen der eigenen Vorgehensweise zu sensibilisieren, wurde in Aufgabe 2) von ihnen gefordert, die beim Lösen der Teilaufgaben verwendeten Regeln und Sätze zu benennen.
Im Folgenden sollen kurz die mathematischen Inhalte benannt werden, auf welche die einzelnen Aufgaben abzielen:
Aufgabe 1: Eigenschaften eines Kreises, Beziehung zwischen den Punkten auf der Kreislinie
Aufgabe 2: Rechnen mit Winkeln (insbesondere Winkeladdition), Winkelsummensatz, Ergänzungswinkel
Aufgabe 3: Gleichschenklige Dreiecke, Basiswinkelsatz, rechte Winkel
Aufgabe 4: Gleichungssysteme lösen (insbesondere mit dem Einsetzungsverfahren)
Entdecken und Formulieren vom Satz des Thales
Die Klasse wird in drei Gruppen geteilt. Gruppe 2 beschäftigt sich mit der Aussage vom Satz des Thales, wohingegen Gruppe 1 und 3 die Umkehrung erforschen.
SchülerInnen der ersten Gruppe erhalten neben dem Aufgabenblatt Overheadprojektor-Folien mit der schon vorgezeichneten Seite c des Dreiecks ABC, s.d. möglichst zügig gearbeitet werden kann. Die SuS sollen sich in der Gruppe austauschen und organisieren, wer welche Winkelgröße \beta in seinem/ihren Dreieck realisiert. Damit es nicht zu viel Folien sind, soll jeder Schüler/ jede Schülern der Gruppe mindestens zwei rechtwinklige Dreiecke mit unterschiedlichen Winkelgrößen für \beta mit Hilfe des Geodreiecks konstruieren. Danach sollen die Folien aufeinander gelegt werden, d.h. die SuS müssen zusammenarbeiten und überlegen, welche Bedingung (Seite c auf Seite c oder Rechte Winkel auf rechte Winkel) sie invariant halten möchten. Durch das Sammeln mehrerer unterschiedlicher, rechtwinkliger Dreieck mit gleicher Hypotenuse sollte die Vermutung der Umkehrung des Satz des Thales wecken, nämlich das der Eckpunkt C auf einer Kreislinie liegen muss (Seite c wird auf Seite c gelegt) oder das die Seiten c Durchmesser eines Kreises sind (Rechte Winkel werden aufeinander gelegt). Am Schluss soll ihre Vermutung auch kurz schriftlich festgehalten werden, damit im weiteren Verlauf der Unterrichtssequenz bei Behandlung der Umkehrung darauf verwiesen und die Vermutung mit dem Umkehrung des Satz des Thales verglichen werden kann.
Gruppe 2 beschäftigt sich mit der Aufgabe, in einen vorgegebenen Halbkreis ein Dreieck ABC eizuzeichnen, dessen Winkel γ möglichst groß sein soll. Je nach Situation kann man diese Aufgabe auch als Wettbewerb verpacken. Ziel ist es, dass die SuS zu dem Schluss kommen, dass dieser Winkel immer 90 Grad beträgt, womit die Aussage des zu zeigenden Satzes motiviert wäre.
Gruppe 3 arbeitet mit einem Applet von Geogebra, welches im Grunde einfach einen Kreis vorgibt. Die SuS sollen verschiedene rechtwinklige Dreiecke in den Kreis einzeichnen, deren Eckpunkte jeweils auf der Kreislinie liegen sollen. Ziel ist es hierbei, dass die SuS zu dem Schluss kommen, dass die Grundseite des rechtwinkligen Dreiecks immer den Durchschnitt des Kreises darstellt.
In jeder der drei Gruppen werden also verschiedene Szenarien behandelt, welche ein Verständnis für und eine Herangehensweise an den Satz des Thales ermöglichen sollen. Im Plenum können die Erkenntnisse der unterschiedlichen Gruppen vorgestellt und diskutiert werden.
Exploration der Phänomensituation (Thalesfiguren)
Beweisfindung und Argumentation
Die Idee ist es, dass SuS mit unterschiedlichen Leistungsniveaus alle einen vollständigen Beweis aufschreiben können. Dafür haben wir uns überlegt, den Beweis in seine logischen Abschnitte zu unterteilen:
- Finden der gleichschenkenkligen Dreiecke
- Dies in Beziehung mit den Winkeln setzen
- Anwenden des Satzes über die Winkelsumme
- Algebraisches Umformen
Wir haben uns dafür entschieden die Fragestellungen recht allgemein zu halten, damit auch (sehr) gute SuS die Möglichkeit haben selbstständig den Beweis ohne zu viele Hilfen zu führen. Stattdessen besteht für schwächere SuS die Möglichkeit sich Hilfskarten zu den einzelnen Schritten anzuschauen. Hier war es unser Ziel möglichst ohne schriftliche Erklärungen zu arbeiten, sondern nur die bekannte Skizze der Situation zu verändern, bzw. bestimmte Teile hervorzuheben. Sollte dies immer noch nicht reichen, können sich SuS dann noch an die Lehrkraft wenden.
Diskussion
Nachdem die einzelnen Teilnehmergruppen ihre Vorschläge zur unterrichtlichen Umsetzung der verschiedenen Bestandteile des Beweisprozesses zum Satz des Thales vorgestellt haben, wird im Plenum über die präsentierten Ergebnisse (Idee, Nutzen, Umsetzung, usw.) diskutiert. Die wesentlichen Diskussionspunkte sollen hier angeführt werden.
1. Aktivierung von Vorwissen
Kritik erntete die Formulierung der Frage im Aufgabenteil 3c), die für SuS vermutlich verwirrend und umständlich erscheint. Ausgehend von dem explizit dargestellten Dreieck sollten die SuS nämlich Aussagen über allgemeine Dreiecke treffen. Daneben erschien die konkrete Benennung der Winkelgröße des in der Skizze bereits eingezeichneten rechten Winkels wenig sinnvoll.
Darüber hinaus wurde darauf hingewiesen, dass das skizzierte Dreieck zu Aufgabe 3 nicht nur ein gleichschenkliges, sondern zusätzlich auch ein rechtwinkliges Dreieck, und damit ein extremer Spezialfall des Dreiecks sei. Sinnvoller sei die "Aufteilung" der Aufgabenstellung bzw. die Verwendung eines gleichschenkligen, aber nicht rechtwinkligen Dreiecks, da die Aufgabe ohnehin eher auf die Eigenschaften von gleichschenkligen Dreiecken abziele.
2. Entdecken und Formulieren vom Satz des Thales
Diskutiert wurden vor allem mögliche Schwierigkeiten, die sich bei den präsentierten Konstruktionsaufgaben für die SuS ergeben könnten: Zum einen wurden Zweifel daran geäußert, inwiefern SuS in der Lage seien, Dreiecke zu einer gegebenen Seitenlänge und den angrenzenden Winkelgrößen zu konstruieren. Darüber hinaus gehen SuS bei Konstruktionsaufgaben zunächst davon aus, nur mit Zirkel und Lineal arbeiten zu dürfen. Eine mögliche Idee wäre deshalb - neben der Bereitstellung von Geodreiecken als Werkzeug - die Voranfertigung von Papierschnipseln mit rechten Winkeln als zusätzliches Werkzeug.
Außerdem wurde eine weitere Methode vorgeschlagen, die sich für diese Beweisphase eignen würde: Mit einer dynamischen Mathematiksoftware (z.B. GeoGebra) könnten SuS bei gegebenen Voraussetzungen vom Satz des Thales (Halbkreis mit eingezeichnetem Durchmesser, der der Grundseite eines Dreieckes entspricht) die dritte, obere Ecke des Dreiecks auf der Kreislinie verschieben und so erfahren, dass der rechte Winkel am Halbkreis auch bei Verschiebung unverändert bleibe.
Generell erschienen die Ideen der Gruppe dennoch sinnvoll. Gelobt wurden vor allem die verschiedenen Möglichkeiten und Richtungen, den Satz des Thales erfahrbar zu machen (Satz und Kehrsatz).
3. Exploration des Phänomensituation (Thalesfiguren)
Positiv hervorgehoben wurde vor allem, dass mit den gestellten Aufgaben das Wiedererkennen der Thalesfigur trainiert und die Bildung von Prototypen vermieden werde.
4. Beweisfindung und Argumentation
Sehr sinnvoll erschien die Strukturierung der Argumentation in vier Arbeitsschritte sowie die innere Differenzierung der Aufgaben. SuS, für die das Anforderungsniveau zu hoch ist, können zusätzliche Hinweise und Hilfestellungen zur Bearbeitung erhalten. Ebenfalls hilfreich und ansprechend erscheint die Verwendung von Skizzen und farblichen Markierungen.