Wurzel aus 2 ist irrational
Aus Geometrie-Wiki
Version vom 31. Oktober 2019, 08:48 Uhr von User123 (Diskussion | Beiträge)
Satz: Die Wurzel aus 2 ist irrational
Annahme: 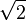 ist rational.
ist rational.
d.h. 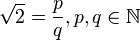 .
.
Beweis durch Widerspruch.
Annahme: 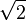 = rational
= rational
D.h.  p,q
p,q 
 :
: 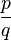 =
= 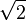 , mit p,q sind teilerfremd.
, mit p,q sind teilerfremd.

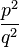 = 2
= 2

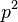 =
= 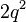
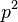 ist gerade.
ist gerade.  p=2n, mit n
p=2n, mit n 


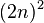 =
= 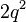

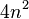 =
= 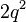

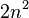 =
= 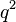
 q ist ebenfalls gerade
q ist ebenfalls gerade  p und q sind nicht teilerfremd.
p und q sind nicht teilerfremd.

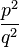 ist kürzbar.
ist kürzbar.

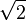 = irrational
= irrational

