Beweise von Studenten

Satz: Wenn ein Viereck ein Rechteck...

Wenn ein Viereck ein Rechteck ist, dann sind seine Diagonalen gleich lang und sie halbieren sich.

1. Idee: Man muss dabei ja 1. die gleichlangen Diagonalen und 2. die sich halbierenden Diagonalen zeigen. Habe aber einfach ein Problem den Beweis zu den gleichlangen Diagonalen zu führen. Hat jemand eine Idee?--Löwenzahn 15:52, 20. Jul. 2010 (UTC)
   

Geht das nicht über SWS? Also wenn du das Rechteck ABCD hast, z.B. die beiden Dreiecke ABD und ABC vergleichen, die müssten laut SWS kongruent sein, damit also auch die Diagonalen. --Ncesi1 15:57, 20. Jul. 2010 (UTC)

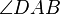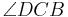Kann ich denn in einem Rechteck davon ausgehen, dass wir einen rechten Winkel bei $\angle DAB$ und $\angle DCB$ haben? Dann würde SWS gehen, das würde ich dann verstehen...--Löwenzahn 16:11, 20. Jul. 2010 (UTC)

Davon kann man natürlich ausgehen, das ist schließlich eins der Merkmale von Rechtecken. Die Kombination der Dreiecke DAB und DCB würde dir aber, wenn ich richtig liege, nicht weiterhelfen, weil du dann nur eine der beiden Diagonalen betrachtest. Du musst also die Dreiecke so wählen, dass beide Diagonalen betrachtet werden (z.B. ABD und ABC). --Ncesi1 16:15, 20. Jul. 2010 (UTC)