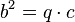Die Satzgruppe des Pythagoras
(ohne Ähnlichkeitsgeometrie)
Die Satzfindung
[ www.youtube.com is not an authorized iframe site ]
Aufgabe 01 21.04.2020
- Richten Sie einen persönlichen Geogebrakanal ein, in dem Sie Ihre Lösungsdateien abspeichern um dann hier die entsprechenden Links einfügen zu können. (geogebra.org)
- Experimentieren Sie selbst mit der entsprechenden Geogebradatei: Pythagoras entdecken.
- Bauen Sie die Datei nach.
- Entwerfen Sie ein Arbeitsblatt mit Arbeitsanweisungen für Realschüler einer neunten Klasse zum Experimentieren mit der Datei.
- Wir beziehen uns auf die Bezeichnungen in der Geogebradatei. Es sei
 der Mittelpunkt von der Mittelpunkt von  . Für den Spezialfall . Für den Spezialfall 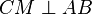 lässt sich der Beweis für den Satz von Pythagoras recht leicht führen. lässt sich der Beweis für den Satz von Pythagoras recht leicht führen.
- a) Führen Sie den Beweis des Satzes von Pythagoras für diesen Spezialfall mathematisch formal korrekt und veröffentlichen Sie den Beweis hier in den Lösungen.
- b) Verdeutlichen Sie einen enaktiven "Beweis" dieses Spezialfalls, wie er von Schülern geführt werden könnte.
Lösungen zu Aufgabe 01 21.04.2020 Elementargeometrie
Aufgabe 02 21.04.2020
- Generieren Sie mit Geogebra eine Datei zur Findung des Höhensatzes.
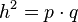
- Generieren Sie mit Geogebra eine Datei zur Findung des Kathetensatzes.
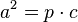 bzw. bzw. 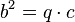
Lösungen zu Aufgabe 02 21.04.2020 Elementargeometrie
Der Beweis
Eines unserer ersten Videos
Mein Beweis für den Pythagoras
[ www.youtube.com is not an authorized iframe site ]
Beweis der ersten binomischen Formel von Prof. Spannagel
erste binomische Formel ikonisch beweisen
Die Version von Alan Kitching (1986): schlicht, knapp, elegant, ästhetisch, ein Meisterwerk
[ www.youtube.com is not an authorized iframe site ]
Manchmal brauchst du keinen Film
Alan Kitching als Geogebradatei
Aufgabe 03 21.04.2020
- Formulieren Sie den Beweis von Alan Kitching mathematisch formal korrekt.
- Beweisen Sie den Höhensatz mittels des Satzes von Pythagoras.
|
 der Mittelpunkt von
der Mittelpunkt von  . Für den Spezialfall
. Für den Spezialfall 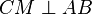 lässt sich der Beweis für den Satz von Pythagoras recht leicht führen.
lässt sich der Beweis für den Satz von Pythagoras recht leicht führen.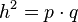
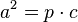 bzw.
bzw.