Lösung von Aufg. 7.3P (SoSe 20)
Aus Geometrie-Wiki
Version vom 8. Juni 2020, 16:58 Uhr von Kohlhoffj (Diskussion | Beiträge)
Gegeben seien drei paarweise verschiedene und kollineare Punkte A, B und C in einer Ebene E. Ferner sei eine Gerade g Teilmenge der Ebene E, wobei keiner der Punkte A, B und C auf g liegen möge. Beweisen Sie folgenden Zusammenhang:
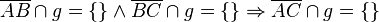
(Hinweis: Nehmen Sie einen weiteren Punkt D an, mit 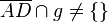 und nutzen Sie den Satz von Pasch)
und nutzen Sie den Satz von Pasch)
Voraussetzung: 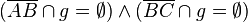
Behauptung: 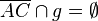
Annahme: 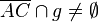
| Beweisschritt | Begründung | |
|---|---|---|
| 1) | 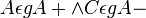 |
Annahme, Satz von Pasch |
| 2) | 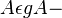 |
1), Voraussetzung, Satz von Pasch |
| 3) | 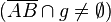 |
1), 2), Satz von Pasch |
| 4) | Widerspruch zur Voraussetzung | 3), Voraussetzung |
--tgksope (Diskussion)
Frage: Wie kann ich + und - "hochstellen"? --tgksope (Diskussion)

