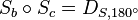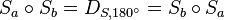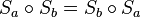Übung 17. Juni Elementargeometrie NAF von Geradenspiegelungen kommutativ gdw senkrecht
Aus Geometrie-Wiki
Version vom 17. Juni 2020, 12:36 Uhr von *m.g.* (Diskussion | Beiträge)
Inhaltsverzeichnis[Verbergen] |
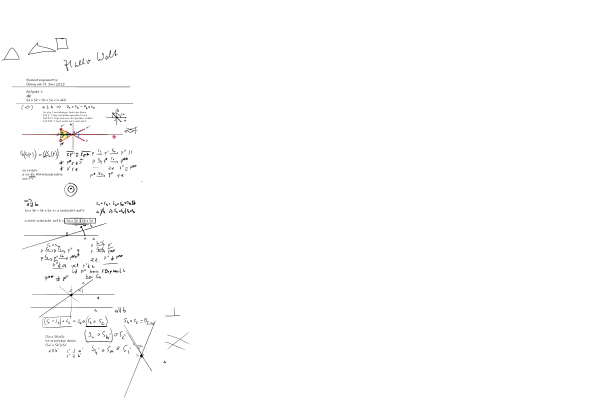
Das Whiteboard zur Übung
Inhalt der Übung
kommutativ gdw senkrecht
Satz:
- Es seien
 und
und  zwei verschiedene Geraden.
zwei verschiedene Geraden.
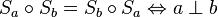
- Es seien
Beweis: aus senkrecht folgt kommutativ
Es sei 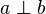 .
.
Zu zeigen 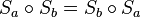
Variante über Drehungen
Sei 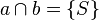 .
.
Der Winkel 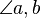 zwischen
zwischen  und
und  hat die Größe
hat die Größe 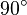 :
:
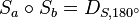
Der Winkel 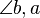 zwischen
zwischen  und
und  hat die Größe
hat die Größe 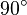 :
: