Lösungen Serie 6 Einführung in die Geometrie SoSe 2020
Inhaltsverzeichnis |
Lösung Aufgabe 6.1
Aufgabe 6.1
Bestimmen Sie die folgenden Mengen:
-
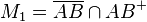 .
.
-
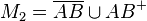 .
.
-
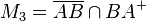 .
.
-
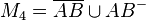 .
.
-
 .
.
-
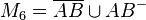 .
.
Lösung
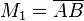
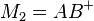
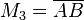

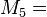 {A}
{A}
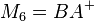
Lösung von Ferrus
Bemerkungen M.G.
Lösung Aufgabe 6.2
Aufgabe
Definieren Sie den Begriff Halbebene 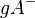 .
.
Lösung
Es sei g eine Gerade, die mit der Ebene E inzidiert.
Die Menge aller Punkte P der Ebene E, für die gilt, dass 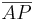 einen Schnittpunkt mit g hat, heißt Halbebene
einen Schnittpunkt mit g hat, heißt Halbebene 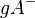 .
.
Lösung Aufgabe 6.3
Aufgabe
Definition: (Dreieck)
- Es gelte
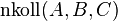 .
.
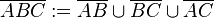 .
.
- Es gelte
Ergänzen Sie die Definition um den Begriff des Inneren des Dreiecks  .
.
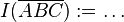 .
.
Lösung
Fehler beim Parsen(Lexikalischer Fehler): I(\overline{ABC}):= {P| zw(B,K,C) \cap zw(A,P,K)} =Lösung Aufgabe 6.4= ==Aufgabe== Beweisen Sie den folgenden Satz:<br /> Satz 6.1. (Schnitt konvexer Mengen)<br /> ::Die Schnittmenge zweier konvexer Mengen ist konvex. ==Lösung== Es seien <math>M_1
undzwei konvexe Punktmengen ...
Lösung Aufgabe 6.5
Aufgabe
Beweisen Sie, dass jede Strecke 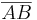 eine konvexe Menge ist.
eine konvexe Menge ist.
Lösung
Lösung 0
Es seien 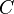 und
und 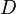 zwei Punkte der Strecke
zwei Punkte der Strecke 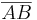 .
.
Wir haben zu zeigen, dass jeder Punkt von ....
eingestellte Lösung 1
Bemerkung --*m.g.* (Diskussion) 17:27, 16. Jun. 2020 (CEST)=
Schritte 4 und 5 sind unnötig. Der Rest ist nicht zwingend.
Sie müssen zeigen, dass ein beliebiger Punkt  von
von 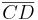 zu
zu 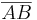 gehört.
gehört.
Für die Endpunkte 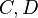 ist das trivial.
ist das trivial.
Sei 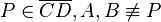 .
.
Wir müssen zeigen, dass 
Das haben wir gezeigt, wenn wir

gezeigt haben.
Wir kümmern uns zunächst um die Lage der Punkte 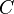 und
und 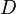 .
.
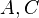 und
und 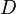 sind drei kollineare paarweise verschiedene Punkte von denen demnach genau einer zwischen den anderen beiden liegt. Sei dieses o.B.d.A. der Punkt
sind drei kollineare paarweise verschiedene Punkte von denen demnach genau einer zwischen den anderen beiden liegt. Sei dieses o.B.d.A. der Punkt 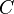 . Über die Punkte und ihre Abstände haben wir nun die folgenden gesicherten Kenntnisse:
. Über die Punkte und ihre Abstände haben wir nun die folgenden gesicherten Kenntnisse:
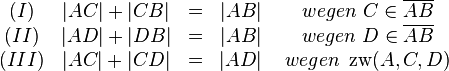
Der Punkt 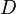 muss nun zwischen
muss nun zwischen 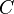 und
und 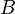 liegen.
liegen.
Wäre dem nicht so, müsste 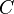 zwischen
zwischen 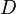 und
und 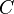 liegen.
liegen.
Hier müssen Sie jetzt einen Widerspruch finden ...
Wegen 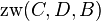 gilt:
gilt:
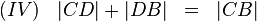
Jetzt konzentrieren wir uns noch mal auf  :
:

Jetzt versuchen Sie, aus (I) bis (V) (*) zu "basteln".
Lösung Aufgabe 6.6
Aufgabe
Gegeben seien in der Ebene  die offene Halbebene
die offene Halbebene 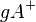 , die Trägergerade
, die Trägergerade  und die offene Halbebene
und die offene Halbebene 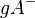 . Sie dürfen davon ausgehen, dass Folgendes bewiesen wurde:
. Sie dürfen davon ausgehen, dass Folgendes bewiesen wurde:
-
 ,
,
-
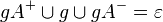 .
.
Satz 6.2 (Halbebenen sind konvex)
- Halbebenen sind konvexe Punktmengen.
Beweisen Sie Satz 6.2.
(Das Axiom von Pasch ist hilfreich)
Lösung 0
Wir beginnen mit der Halbebene 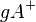 .
.
Es seien nun  und
und 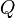 zwei Punkte aus
zwei Punkte aus 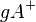 .
.
Wir haben zu zeigen, dass .....
1. Lösung, die eingestellt wurde
Lösung Aufgabe 6.7
Aufgabe
Beweisen Sie, dass das Innere eines Dreiecks konvex ist.
Lösung
Nach Definition ist das Innere eines Dreiecks die Schnittmenge der drei Halbebenen 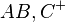
, 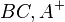 und
und 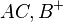 .
Weil Halbebenen nach Satz 6.2 konvex sind
.
Weil Halbebenen nach Satz 6.2 konvex sind
und nach Satz 6.1 die Schnittmenge zweier konvexer Mengen auch konvex ist,
ist das Innere eines jeden Dreiecks konvex.
Lösung Aufgabe 6.8
Aufgabe
Definieren Sie die folgenden Begriffe:
- Kreis
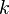 mit Mittelpunkt
mit Mittelpunkt 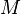 und Radius
und Radius  .
.
- Halbkreis mit den Endpunkten
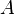 und
und 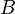 .
.
- Viertelkreis mit den Endpunkten
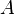 und
und 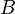 .
.
(Halbebenen und Schnittmengen sind hilfreich)
Lösung
Lösung Aufgabe 6.9
Aufgabe
Definieren Sie den Begriff Inneres eines Kreises und beweisen Sie, dass das Innere eines Kreises konvex ist.
Lösung
Definition
Es sei 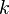 ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt 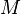 und dem Radius
und dem Radius  .
.
Das Innere 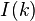 des Kreises
des Kreises 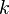 wird wie folgt definiert:
wird wie folgt definiert:
 .
.
Beweis des Satzes
Satz:  .
.
Für jeden Punkt  ist also zu zeigen, dass
ist also zu zeigen, dass 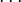 .
.
Wir nehmen an, dass ....
Wegen  gilt die folgende Gleichung ... .
gilt die folgende Gleichung ... .
...
Lösung Aufgabe 6.10
Aufgabe
Ebene Geometrie:\\
Definition: (Ellipse)
- Es seien
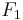 und
und  zwei Punkte und
zwei Punkte und  eine beliebige aber feste positive reelle Zahl. Die folgende Punktmenge
eine beliebige aber feste positive reelle Zahl. Die folgende Punktmenge 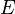 heißt Ellipse mit den Brennpunkten
heißt Ellipse mit den Brennpunkten 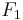 und
und  :
: 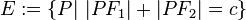
- Es seien
Lassen Sie mit Geogebra einen Kreis 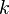 mit dem Mittelpunkt
mit dem Mittelpunkt 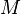 und dem Radius
und dem Radius  zeichnen. Konstruieren Sie dann einen Punkt
zeichnen. Konstruieren Sie dann einen Punkt 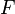 im Inneren von
im Inneren von 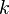 . Legen Sie nun einen Punkt
. Legen Sie nun einen Punkt 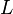 auf
auf 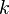 fest. Lassen Sie die Mittelsenkrechte
fest. Lassen Sie die Mittelsenkrechte 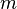 von
von 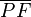 zeichnen und bestimmen sie den Schnittpunkt
zeichnen und bestimmen sie den Schnittpunkt  von
von 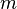 mit
mit 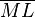 .
Beweisen Sie, dass jeder Schnittpunkt
.
Beweisen Sie, dass jeder Schnittpunkt  ein Punkt einer Ellipse mit den Brennpunkten
ein Punkt einer Ellipse mit den Brennpunkten 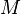 und
und 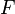 und
und  ist.
ist.





