Lösung von Aufg. 7.3P (SoSe 20)
Aus Geometrie-Wiki
Version vom 23. Juli 2020, 11:27 Uhr von Kohlhoffj (Diskussion | Beiträge)
Gegeben seien drei paarweise verschiedene und kollineare Punkte A, B und C in einer Ebene E. Ferner sei eine Gerade g Teilmenge der Ebene E, wobei keiner der Punkte A, B und C auf g liegen möge. Beweisen Sie folgenden Zusammenhang:
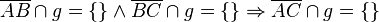
(Hinweis: Nehmen Sie einen weiteren Punkt D an, mit 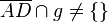 und nutzen Sie den Satz von Pasch)
und nutzen Sie den Satz von Pasch)
Voraussetzung: 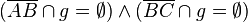
Behauptung: 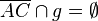
Annahme: 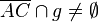
| Beweisschritt | Begründung | |
|---|---|---|
| 1) | 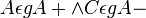 |
Annahme, Satz von Pasch |
| 2) | 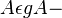 |
1), Voraussetzung, Satz von Pasch |
| 3) | 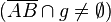 |
1), 2), Satz von Pasch |
| 4) | Widerspruch zur Voraussetzung | 3), Voraussetzung |
--tgksope (Diskussion)
Ich kann deinem Beweis leider nicht ganz folgen. Kannst du vielleicht eine Skizze dazu hochladen? Somit kann ich es besser nachvollziehen! Und hast du beachtet, dass die Punkte A, B und C auf einer Geraden liegen (kollineare Punkte)? Um den Beweis zu führen, nutze den Hinweis. Damit geht es schnell und einfach. Da brauchst du auch kein Widerspruchbeweis führen, sondern einen direkten Beweis. --Tutorin Laura (Diskussion) 11:52, 9. Jun. 2020 (CEST)
Frage: Wie kann ich + und - "hochstellen"? --tgksope (Diskussion)
Oben in der Leiste bei "Format" ist ein x2. Darauf klicken und dazwischen das einfügen, was hochgestellt werden soll. --Tutorin Laura (Diskussion) 11:41, 9. Jun. 2020 (CEST)
Voraussetzung: 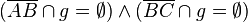
Behauptung: 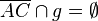
Zusatz: Es sei ein Punkt D mit: 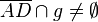
| Beweisschritt | Begründung | |
|---|---|---|
| 1) | 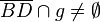 |
Zusatz, Vor., Satz von Pasch, Existenz des Dreiecks 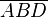
|
| 2) | 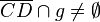 |
1), Vor., Satz von Pasch, Existens des Dreiecks 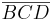
|
| 3) | 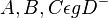 |
Zusatz, 1), 2), Def. Halbebene |
| 4) | 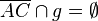 |
3), Def. Halbebene |

