Lösung von Aufgabe 11.1P (SoSe 20)
Aus Geometrie-Wiki
Version vom 25. Juli 2020, 09:58 Uhr von Kohlhoffj (Diskussion | Beiträge)
Beweisen Sie Satz IX.4:
Bei einer Punktspiegelung werden Geraden stets auf parallele Bildgeraden abgebildet.
Voraussetzung: Punktspiegelung einer Geraden g
Behauptung: g parallel zu g
Zusatz: a und b sind die Spiegelgeraden der Punktspiegelung mit: 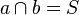 und
und 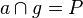 und
und 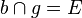
| Beweisschritt | Begründung | |
|---|---|---|
| 1) | 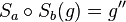 |
Geradentreue der Geradenspiegelung, Def. Punktspiegelung |
| 2) | 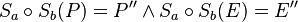 |
Def. Punktspiegelung, S ist Fixpunkt |
| 3) | 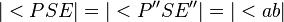 |
Winkelmaßerhaltung der Geradenspiegelung, 2), Zusatz |
| 4) | 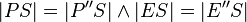 |
Eigenschaft Punktspiegelung, 2) |
| 5) | 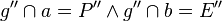 |
1), 2), 3), Eigenschaft Geradenspiegelung, Zusatz |
| 6) | 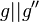 |
3), 4), 5) |
--tgksope (Diskussion) 10:58, 25. Jul. 2020 (CEST)

