Vorlesung 0: Satz des Pythagoras
Motivierung des Satzes
Der Satz des Pythagoras ist wohl der mathematisches Satz, von dem die meisten Menschen schon einmal gehört haben. Insofern ist es relativ leicht, die Behandlung dieses Satzes im Mathematikunterricht der Schule zu motivieren: Man möchte schon wissen, was es mit diesem vom Namen her bekannten Satz auf sich hat. Hier eine nicht unbedingt ernst zu nehmende Einstimmung.
[ www.youtube.com is not an authorized iframe site ]
Warnung: Wir haben dieses Video für unser damaliges Projekt Mathe-MOOC, Mathematisch Denken gemacht. Dieses Projekt hatte Erwachsene als Zielgruppe. Bei Schülerinnen und Schülern in der Pubertät kommen solche mehr oder weniger albernen Videos häufig nicht gut an: Das Ganze ist für diese Altersgruppe eventuell zu kindisch. Wenn die Pubertät vorbei ist, wird sowas wieder als spaßig und zumindest akzeptabel empfunden. Wenn Sie das Video später im eigenen Unterricht einsetzen wollen (was Sie gern tun dürfen) sollten Sie sich sicher sein, dass es für Ihre speziellen Schülerinnen und Schüler nicht zu albern ist.
Satzfindung
Satzfindung mittels funktionaler Betrachtungen und Grenzfallbetrachtungen
[ www.youtube.com is not an authorized iframe site ]
Überprüfung der Vermutung
Jeder Schüler zeichnet ein rechtwinkliges Dreieck und überprüft durch Messung und Rechnung, ob die Vermutung stimmen könnte.
Aufgaben zur Übung
- Generieren Sie mit Geogebra eine Datei zur Findung des Höhensatzes.
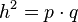
- Generieren Sie mit Geogebra eine Datei zur Findung des Kathetensatzes.
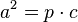 bzw.
bzw. 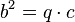
Der Beweis
Mein Beweis für den Pythagoras
[ www.youtube.com is not an authorized iframe site ]
Der Beweis selbst stammt natürlich nicht von mir, sondern von dem indischen Mathematiker Bhaskara: [1]
Beweis der ersten binomischen Formel von Prof. Spannagel
erste binomische Formel ikonisch beweisen
Die Version von Alan Kitching (1986): schlicht, knapp, elegant, ästhetisch, ein Meisterwerk
[ www.youtube.com is not an authorized iframe site ]
Manchmal brauchst du keinen Film
Alan Kitching als Geogebradatei
Übungsaufgaben
- Formulieren Sie den Beweis von Alan Kitching mathematisch formal korrekt.
- Beweisen Sie den Höhensatz mittels des Satzes von Pythagoras.

