Relationen WS 20 21

Relationen

Beispiele

Halt dich senkrecht

Flag of Switzerland (Pantone)

Im Schulpraktikum war der Begriff der Senkrechten zu behandeln. Der Praktikant hatte ein Bild der Schweizer Nationalflagge auf eine Folie gedruckt und fragte die Schüler, welche Linien Senkrechte wären. Bei den Schülern stellte sich nach den ersten Antworten leichte Unsicherheit ein.
Der Grund für diese Unsicherheit: Die Frage des Praktikanten war völlig unsinnig. Eine Antwort wie Gerade $a$ steht senkrecht ist lediglich eine Aussageform, der kein Wahrheitswert zuzuordnen ist. Erst wenn man die Lage von $a$ bezüglich einer anderen Geraden $b$ (Ebene, Strahl, Strecke) betrachtet, ist es sinnvoll davon zu sprechen, dass $a$ eine Senkrechte ist.
Die Relation Gerade $a$ steht senkrecht auf Gerade $b$ ist zweistellig.

Eine klassische Dreiecksbeziehung

Tom ist der Liebhaber von Gabi. Zu der Ehre der Liebhabereigenschaft kommt er durch die Existenz von Frank, dem Ehemann von Gabi. Tom, Gabi und Frank stehen in einer dreistelligen Relation zueinander, der klassischen Dreiecksbeziehung.
Wir könnten diese Relation auch so formulieren: Gabi steht zwischen zwei Männern.

Beispiel 3

Trauen Sie sich: Präsentieren Sie hier ein eigenes Beispiel.

Ein Quiz zwischendurch

Pluspunkt für eine richtige Antwort:
Minuspunkte für eine falsche Antwort:
Ignoriere den Fragen-Koeffizienten:

1. Setzen Sie ein Häckchen, wenn es sich um eine zweistellige Relation handelt

	Eine Ebene $\alpha$ steht senkrecht zu einer Ebene $\beta$.
→	klar, wie bei Beispiel 1 für Geraden
	Der Punkt $B$ liegt zwischen den Punkten $A$ und $C$.
→	dreistellig
	Von zwei Punkten ein und derselben Geraden liegt einer vor dem anderen.
→	Jetzt werden nur zwei Punkte verglichen.

Punkte: 0 / 0

Definition des Begriffs der Relation

Definition: (n-stellige Relation)

Es seien 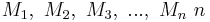$M_1,\ M_2,\ M_3,\ ...,\ M_n\ n$ Mengen, wobei keine dieser Mengen die leere Menge ist. Jede Teilmenge aus 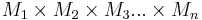$M_1 \times M_2 \times M_3 ...\times M_n$ ist eine 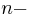$\ n-$stellige Relation.