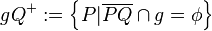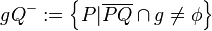Die Axiome der Anordnung
Inhaltsverzeichnis
|
Streckenantragen und das Axiom vom Lineal
Halbebenen und das Axiom von Pasch
Halbebenen
Analogiebetrachtungen
Die folgenden Lückentexte können Sie auch als Übungsblatt im pdf-Format herunterladen: Übungsblatt Halbgeraden/-ebenen
Wir konstatieren:
- Eine Gerade wird durch einen ......Punkt ...... in zwei .....Halbgeraden....... eingeteilt.
- Eine Ebene wird durch eine ....Gerade ........ in zwei ...Halbebenen......... eingeteilt..
- Eine Gerade wird durch einen ......Punkt ...... in zwei .....Halbgeraden....... eingeteilt.
- Eine Gerade ist ein .ein....dimensionales Objekt.
- Eine Ebene ist ein .zwei....dimensionales Objekt
- Eine Gerade ist ein .ein....dimensionales Objekt.
- Im Fall dieser Geradenteilung ist der Trenner ein ..null...dimensionales geometrisches Objekt
- Im Fall dieser Ebenenteilung ist der Trenner ein .ein....dimensionales geometrisches Objekt.
- Im Fall dieser Geradenteilung ist der Trenner ein ..null...dimensionales geometrisches Objekt
- Wenn also n die Dimension des geometrischen Objekts ist, das geteilt wird, dann hat der Trenner die Dimension ..n-1... .
Geradenteilung:
- Es seien
 eine Gerade und
eine Gerade und 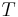 ein Punkt auf ihr. Ferner sei
ein Punkt auf ihr. Ferner sei 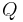 ein von
ein von 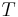 verschiedener Punkt der Geraden
verschiedener Punkt der Geraden  . Die Menge
. Die Menge  wird durch durch den Trenner
wird durch durch den Trenner 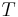 in genau zwei Klassen eingeteilt:
in genau zwei Klassen eingeteilt:
- Die Menge aller Punkte von
 , die mit
, die mit 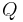 auf derselben .Halbgeraden.. .
auf derselben .Halbgeraden.. .
- Die Menge aller Punkte von
 , die mit
, die mit 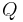 nicht auf derselben ..Halbgeraden. .
nicht auf derselben ..Halbgeraden. .
- Die Menge aller Punkte von
Ebenenteilung:
- Es seien
 eine Ebene und
eine Ebene und 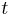 eine Gerade, die vollständig in
eine Gerade, die vollständig in  liegt. Ferner sei
liegt. Ferner sei 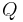 ein nicht zu
ein nicht zu 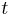 gehörender Punkt der Ebene
gehörender Punkt der Ebene  . Die Menge
. Die Menge  wird durch durch den Trenner
wird durch durch den Trenner 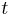 in genau zwei Klassen eingeteilt:
in genau zwei Klassen eingeteilt:
- Die Menge aller Punkte von
 , die mit
, die mit 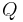 auf derselben ..Halbebene. .
auf derselben ..Halbebene. .
- Die Menge aller Punkte von
 , die mit
, die mit 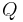 nicht auf derselben .Halbebene.. .
nicht auf derselben .Halbebene.. .
- Die Menge aller Punkte von
Definition des Begriffs der Halbebene
Alles hat zwei Seiten oder grundlegende Ideen der Beschaffenheit von Ebenen
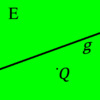
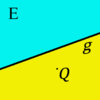
Zu unsere Vorstellung von der Eigenschaften einer beliebigen Ebene  gehört u.a., dass jede Gerade gehört u.a., dass jede Gerade  , die zu unserer jeweiligen Ebene , die zu unserer jeweiligen Ebene  gehört, diese in zwei Hälften bzw. zwei Seiten einteilt. Zur Kennzeichnung der beiden Seiten von gehört, diese in zwei Hälften bzw. zwei Seiten einteilt. Zur Kennzeichnung der beiden Seiten von  bezüglich der Geraden bezüglich der Geraden  verwenden wir einen Punkt verwenden wir einen Punkt 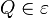 , welcher nicht zu , welcher nicht zu  gehören sollte. gehören sollte.
|
|
Zu der einen Hälfte von  bezüglich bezüglich  gehören alle die Punkte aus gehören alle die Punkte aus 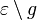 , die mit , die mit 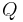 auf derselben Seite von auf derselben Seite von  liegen. Alle anderen Punkte aus liegen. Alle anderen Punkte aus 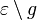 gehören zur anderen Seite von gehören zur anderen Seite von  bezüglich bezüglich  . .
|
|
Offene Halbebenen
Die beiden Seiten, in die die Menge der Punkte einer Ebene  , die nicht auf einer Geraden
, die nicht auf einer Geraden  dieser Ebene liegen, durch diese Gerade
dieser Ebene liegen, durch diese Gerade  eingeteilt wird, heißen offene Halbebenen von
eingeteilt wird, heißen offene Halbebenen von  bezüglich der Trägergeraden
bezüglich der Trägergeraden  . Der nicht zu
. Der nicht zu  gehörende Referenzpunkt
gehörende Referenzpunkt 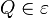 bietet uns eine Möglichkeit zur Bezeichnung der beiden offenen Halbebenen. Die offene Halbebene, zu der alle Punkte gehören, die bezüglich
bietet uns eine Möglichkeit zur Bezeichnung der beiden offenen Halbebenen. Die offene Halbebene, zu der alle Punkte gehören, die bezüglich  mit
mit 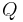 auf derselben Seite liegen, wird mit
auf derselben Seite liegen, wird mit 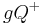 bezeichnet, die andere offene Halbebene von
bezeichnet, die andere offene Halbebene von  bezüglich
bezüglich  und
und 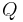 mit
mit 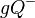 .
.
Obige Ausführungen können als informelle Definition des Begriffs offene Halbebene dienen. Hinsichtlich wirklicher mathematischer Exaktheit der Festlegung, was denn eine offene Halbene sein möge, bedarf es einer genauereren Erklärung, was denn darunter zu verstehen wäre, dass zwei Punkte  und
und 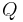 einer Ebene
einer Ebene  auf ein und derselben bzw. auf zwei verschiedenen Seiten dieser Ebene bezüglich einer Geraden
auf ein und derselben bzw. auf zwei verschiedenen Seiten dieser Ebene bezüglich einer Geraden  liegen.
liegen.
Definition IV.1: (offene Halbebene)
- Es sei
 eine Ebene in der die Gerade
eine Ebene in der die Gerade  liegen möge. Ferner sei
liegen möge. Ferner sei 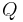 ein Punkt der Ebene
ein Punkt der Ebene  , der nicht zur Geraden
, der nicht zur Geraden  gehört.
gehört.
Unter den offenen Halbebenen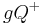 und
und 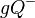 bezüglich der Trägergeraden
bezüglich der Trägergeraden  versteht man die folgenden Teilmengen der Ebene
versteht man die folgenden Teilmengen der Ebene  ohne die Gerade
ohne die Gerade  :
:
- Es sei
Halbebenen
Vereinigt man die Menge der Punkte einer offenen Halbeben mit der Menge der Punkte der Trägergerade so erhält man eine Halbebene.
Definition IV.2: (Halbebene)
- Es sei
 eine Gerade der Ebene
eine Gerade der Ebene  .
. 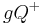 und
und 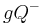 seien die beiden offenen Halbebenen von
seien die beiden offenen Halbebenen von  bezüglich
bezüglich  . Unter den (geschlossenen) Halbebenen von
. Unter den (geschlossenen) Halbebenen von  bezüglich
bezüglich  versteht die beiden Punktmengen, die durch die Vereinigung jeder dieser beiden offenen Halbebene von
versteht die beiden Punktmengen, die durch die Vereinigung jeder dieser beiden offenen Halbebene von  bezüglich der Geraden
bezüglich der Geraden  mit jeweils dieser Geraden
mit jeweils dieser Geraden  entstehen.
entstehen.
- Es sei
Bemerkung: Für die formale Beschreibung von offenen und geschlossenen Halbebenen wird jeweils dieselbe Bezsichnung verwendet: offene Halbebene: 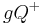 , (geschlossene) Halbebene:
, (geschlossene) Halbebene: 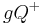 . Der weitere Gebrauch der Sprache kennzeichnet, ob es sich um eine offene oder um die geschlossene Halbene handeln soll. Aus Gründen der Vereinfachung sei vereinbart, dass
. Der weitere Gebrauch der Sprache kennzeichnet, ob es sich um eine offene oder um die geschlossene Halbene handeln soll. Aus Gründen der Vereinfachung sei vereinbart, dass 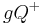 bzw.
bzw. 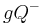 immer die geschlossene Halbebene meint. Soll die offene Halbebene gemeint sein, so ist dieses durch den Zusatz "offen" zu kennzeichnen.
immer die geschlossene Halbebene meint. Soll die offene Halbebene gemeint sein, so ist dieses durch den Zusatz "offen" zu kennzeichnen.
Definition IV.3: Halbraum
Gegeben sei eine Ebene  .
.
- Halbraum
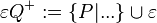
- Halbraum
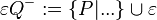
- Halbraum
Das Axiom von Pasch
- Was Axiomatik ist und wie man Axiome zu formulieren hat, das ist erst gegen Ende des 19. Jh. von Pasch gezeigt worden; von ihm lernten es die italienischen Geometer und lernte es Hilbert.
Hans Freudenthal, Mathematik als pädagogische Aufgabe, Stuttgart 1973, S. 14)
- Was Axiomatik ist und wie man Axiome zu formulieren hat, das ist erst gegen Ende des 19. Jh. von Pasch gezeigt worden; von ihm lernten es die italienischen Geometer und lernte es Hilbert.
Axiom III.2: Das Axiom von Pasch
- Gegeben sei ein Dreieck
 . Ferner sei
. Ferner sei  eine Gerade, die durch keinen der drei Eckpunkte
eine Gerade, die durch keinen der drei Eckpunkte 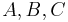 geht. Wenn
geht. Wenn  eine der drei Seiten des Dreiecks
eine der drei Seiten des Dreiecks  schneidet, dann schneidet
schneidet, dann schneidet  genau eine weitere Seite des Dreiecks
genau eine weitere Seite des Dreiecks  .
.
- Gegeben sei ein Dreieck
 die Menge aller Punkte ist, die zwischen
die Menge aller Punkte ist, die zwischen  und
und 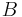 liegen. Vereinigt man diese Menge mit der Menge der beiden Endpunkte
liegen. Vereinigt man diese Menge mit der Menge der beiden Endpunkte 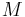 hat.
hat. 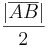 hat.
hat.
 )
)
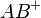 . Nach unserer Vorstellung von Halbgeraden können wir je zwei Punkten von
. Nach unserer Vorstellung von Halbgeraden können wir je zwei Punkten von 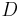 auf
auf 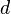 hat. Bei Konstruktionsaufgaben finden wir diese Idee im Zusammenhang mit dem Streckenantragen wieder.
hat. Bei Konstruktionsaufgaben finden wir diese Idee im Zusammenhang mit dem Streckenantragen wieder.



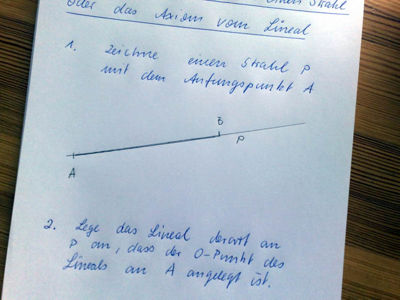
 genau einen Punkt, der zum Anfangspunkt von
genau einen Punkt, der zum Anfangspunkt von 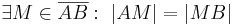 .
.

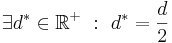
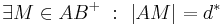
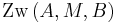 und damit
und damit 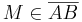

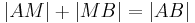
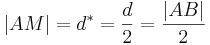 )
)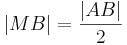
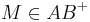 möge gelten:
möge gelten: 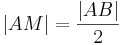
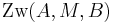 .
.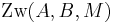
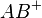 )
)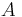 und
und 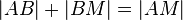
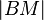
 und
und 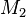 .
.