Lösung von Aufgabe 11.5P (WS 20 21)
Aus Geometrie-Wiki
Version vom 28. Januar 2021, 18:15 Uhr von Werzdavid (Diskussion | Beiträge)
- Gegeben sei ein Winkel
 und ein Punkt P im Inneren des Winkels der nicht auf einem der Schenkel des Winkels
und ein Punkt P im Inneren des Winkels der nicht auf einem der Schenkel des Winkels  liegt. Konstruieren Sie eine Strecke
liegt. Konstruieren Sie eine Strecke  deren Endpunkte D und E jeweils auf einem der beiden Schenkel des Winkels
deren Endpunkte D und E jeweils auf einem der beiden Schenkel des Winkels  liegen und P Mittelpunkt der Strecke
liegen und P Mittelpunkt der Strecke  ist.
ist.
- Beweisen Sie, dass Ihre Konstruktion richtig ist.
Mein Lösungsvorschlag --Werzdavid (Diskussion) 18:15, 28. Jan. 2021 (CET):
| Bemerkung: Ich habe in meiner Lsöung die Punkte A und B vertauscht ;) |
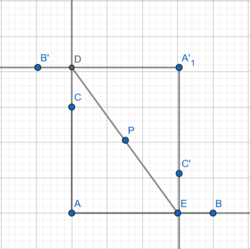
- Vorgehen:
- Ich dachte, dass der Punkt
 zu den beiden Endpunkten der Strecke
zu den beiden Endpunkten der Strecke  den selben Abstand haben muss. Daher könnte man
den selben Abstand haben muss. Daher könnte man  an
an  auf
auf  spiegeln.
spiegeln.
- Als Konsequenz daraus müsste, wenn
 auf
auf 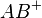 liegt,
liegt,  auf
auf 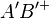 liegen.
liegen.
- Genaus müsste umgekehrt, wenn
 auf
auf 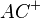 liegt,
liegt,  auf
auf 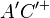 liegen.
liegen.
- Die Spiegelung von
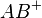 und
und 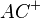 an
an  mit
mit 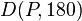 erzeugte jeweils einen Schittpunkt.
erzeugte jeweils einen Schittpunkt.
- Diese habe ich als
 und
und  gekennzeichnet.
gekennzeichnet.
- Nun muss nurnoch die Strecke
 eingezeichnet werden.
eingezeichnet werden.