Lösung von Aufgabe 13.4
Aus Geometrie-Wiki
Version vom 24. Juli 2010, 14:25 Uhr von TheGeosi (Diskussion | Beiträge)
Satz XII.5: (Starker Außenwinkelsatz)
- Jeder Außenwinkel eines Dreiecks ist so groß, wie die Summe der größen der beiden nicht anliegenden Innenwinkel dieses Dreiecks.
Versuch 1
VSS: Dreieck  ,
,  ,
,  ,
, 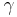 sind Innenwinkel des Dreiecks,
sind Innenwinkel des Dreiecks, 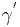 ist nichtanliegender Außenwinkel zu
ist nichtanliegender Außenwinkel zu  und
und 
Beh: 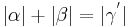
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 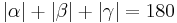
|
(Innenwinkelsumme im Dreieck) |
| (II) | 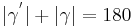
|
(Def. Nebenwinkel), (Supplementaxiom) |
| (III) | 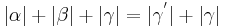
|
(I), (II), (rechnen mit reellen Zahlen) |
| (IV) | 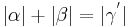
|
(III), (rechnen mit reellen Zahlen) |
--> Beh wahr. qed
--Löwenzahn 09:16, 17. Jul. 2010 (UTC)
Anmerkung
Nur ne Formale Anmerkung:
Ich würde die Behauptung noch allgemeiner definieren und dann später vor Beweisbeginn sagen o.B.d.A. usw....
weiß ja nicht, wie viel Wert später auf die Form gelegt wird... aber wer weiß das schon? Wir werdens dann schon feststellen.

